算术化是将计算编码为代数约束满足问题的过程。这将检验其正确性的复杂性降低到少量概率代数检查。在证明系统中,算术化的选择会影响IOP的选择范围
## 一、高效密码学运算傅里叶变换可以将一个信号分 解成一系列正弦和余弦函数的叠加。
离散傅里叶变换(DFT):
其中一个应用场景:每个约束都是一个多项式,可利用DFT做到整合成一个多项式且保证信息不丢失。
- 称
$𝑥^𝑛 = 1$ 在复数意义下的解是 𝑛 次复根。 - 这样的解有 𝑛 个,称这 𝑛 个解都是 𝑛 次 单位根 或 单位复根 (the 𝑛-th root of unity)。
- 根据复平面的知识,𝑛 次单位根把单位圆 𝑛 等分。
如复平面所示为
$x^3 -1$ 的三次单位根等分情况($x=1$ 旋转$0$ ,$\frac{2π}{3}$ ,$\frac{4π}{3}$ )
数学难问题知识补充:
P: 表示可以由确定性图灵机,确定在多项式时间内解决的判定问题,这也是目前经典计算机的运算能力。
NP:由非确定性图灵机可以在多项式时间内解决的判定问题,不确定有没有多项式解决算法,但可以通过验证的方法得出正确解,所有的P问题都是NP问题。
NP-Hard:如果所有 NP 类问题都可以在多项式时间内规约到问题 H,那么问题 H 是 NP-hard 的。NP-Complete:如果一个问题,既是NP类问题,又是NP-hard问题,这是零知识证明的基础。
难度:DLP > CDH > DDH
离散:有限域而非实数域,但需要注意,不是所有的离散对数问题都是困难的。
应用:
- 椭圆曲线
- DH密钥交换协议,在不安全的通道,通过 shared secret 建立安全的传输。
-
符合完美零知识(见下文区别中介绍),最后的
$z$ 中,$r$ 的随机性保护了$s$ 。Schnorr的签名方案是一个经典的Sigma协议,具有Special Honest-Verifier Zero-knowledge property。
属于功能性问题,功能性问题的回答不止 YES/NO,可以是一个数或是其它。如「求两个数的和」就是一个功能性问题。
只能用 YES/NO 回答的问题,本质上是判断是否属于某一种语言(是一个抽象的概念,通常意义上的字符串是语言,所有的有向无环图也可以是一个语言)。

本质是一个方程组,由一个 R1CS 是一个由三个向量构成的向量组
是一种将语句转换为多项式上二次方程组的方式,它们可以通过线性交互式证明LIPs、代数IOPs、多线性IOPs 等不同信息论协议进行检验。
QAP 实现了与 R1CS 完全相同的逻辑,只不过使用的是多项式而不是向量内积。任何具有乘性复杂度
一个度数(多项式最高次)为
丨:整除
此外,在转换的同时会构建一个对应于代码输入的解(又称为 QAP 的 Witness),之后再基于这个 Witness 构建一个实际的零知识证明系统
以IsZero()判零函数(见算术点路应用章节a.①)为例,或从
comparators.circom中获取的IsZero电路。
out <== −in * inv + 1
in * out === 0
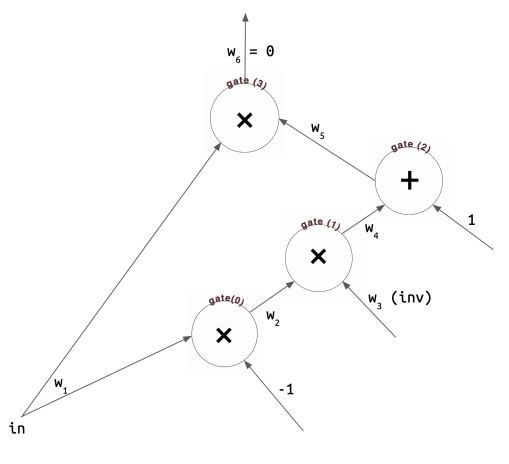
“展平” 为四个约束条件(在算术电路表示中,每个约束条件对应于一个加法或乘法门),每个都采用 左侧 · 右侧 = output 的形式:
g:门gate
$𝑔_0: 𝑤_1 · −1 = 𝑤_2$ $𝑔_1:𝑤_2 · 𝑤_3 = 𝑤_4$ $𝑔_2: (𝑤_4 + 1) · 1 = 𝑤_5$ $𝑔_3: 𝑤_1 ⋅ 𝑤_5 = 𝑤_6$
为满足

分别收集三个线路向量到矩阵
不管结果多简单,过程是复杂的,要验算的东西即组成的多项式也很复杂,所有的中间变量都会成为输入。
注:circom是从代码到R1CS,他下面还有个 snarkjs工具框架,将R1CS生成QAP
将度数
在每个变量
其中,在构造
拉格朗日插值:
注意实际运行时有限域,无小数
- 找到一个多项式,经过四个关键点
- 当处在某个控制点
$x_i$ 的情况下,除了该点有值,其他的控制点值为0
实际是多个多项式相加而得,$y_i$ 为缩放系数,给定点和评估

注:得出一个多项式,就成了上节承诺方案的输入
R1CS生成不一定是QAP,根据不同框架,这里是到AIR,相当于分别是不同的算术化方法
代数中间表示(Algebraic Intermediate Representation, AIR),是由一组均匀计算(uniform computations,均匀性是指数据或分布的相似程度。在统计学中,均匀性的计算通常是指方差或标准差)组成的程序表示,是 StarkWare 在其虚拟机 Cairo 中使用的算术化过程。
AIR框架数学上实现简单,构建出那么一个表格(轨迹矩阵,像机器语言底层系统,故也有的称AIR为机器计算),所有多项式乘在一起就得出唯一多项式。
- 计算执行轨迹。表示为执行迹矩阵 T ,行表示在给定时间点的计算状态,列对应于一个代数寄存器在所有计算步骤中的状态变化。
- 转换程序。约束了迹矩阵 T 两行或多行之间的关系。
- 边界约束。确保了执行中某些单元格和特定常量之间的相等关系。
表格高度是固定的,像circom在运行时不可变更(树的高度固定)
| Step | a | b |
|---|---|---|
| i=1 | 1 | 1 |
| i=2 | 2 | 3 |
| i=3 | 5 | 8 |
| i=4 | 13 | 21 |
我们可以使用两个状态转换多项式来指定 Fibonacci 数列的 AIR 程序:
例如,我们可以检查在第 i=2 行状态转换是否成立:
带预处理的AIR,以在转换程序中同时启用乘法和加法。
带预处理的随机化AIR,以实现多重集合相等性检查。允许交互轮次引入验证器随机性
针对AIR框架,STARK、SNARK(一开始NIZK用得最多,后面加的succint性质)是人为定义的schema,是一种性质,不是很具体的框架,STARK提出者(公司STARKNET)底层用的AIR,同时可以认为STARK也属于SNARK一种实现方式
通常见到AIR就是已经封进了ZKVM中,可以实现传统代码,像StarkNet的Cairo,开放给用户来写代码,不涉及到AIR底层
算术化步骤:
将待验证计算问题转换为检查某个多项式,分两步:
-
第一步
-
构建执行踪迹表格
-
用多项式描述表格中各行/列间的数学关系
-
第二步: 将这两个对象转换为一个低次多项式
-
利用纠错码将执行轨迹转为多项式
哪怕仅一处错误的执行轨迹,会被纠错码放大,以至于与原执行轨迹几乎完全不同
-
-
扩展至更大的域
-
用多项式约束将其转为低次多项式