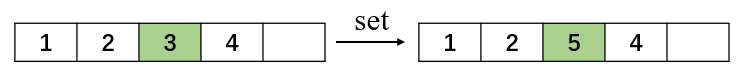[TOC]
同数组不用，数组的大小在定义时已经确定，而在实际过程中数组需要根据数据量的大小自动更改数组大小。底层实现仍是数组，只是将数组进行封装，可以实现自适应的数组Array。
涉及的所有函数方法：
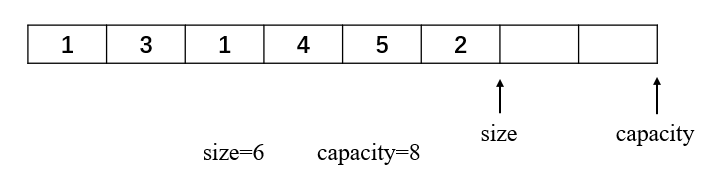
数组无非涉及增、查、改、删四种操作，查和改操作与平常数组操作相同。难点就在于增加元素和删除元素上。对于一般数组当索引index + 1 超过数组大小是就会报错。为了可以根据数据大小改变数组大小，引入capacity（容器）的概念。其中capacity >= size。如图
注： 实际上capacity才是真正数组的大小，size只是capacity中存储数据的多少。 下面分别说一下增删改查的的实现思路
如果增加后 size <= capacity 则直接将数据添加到数组中，如果增加后 size > capacity 则需要对数组进行扩容操作。扩容的方式也就是扩大为原来的2倍。
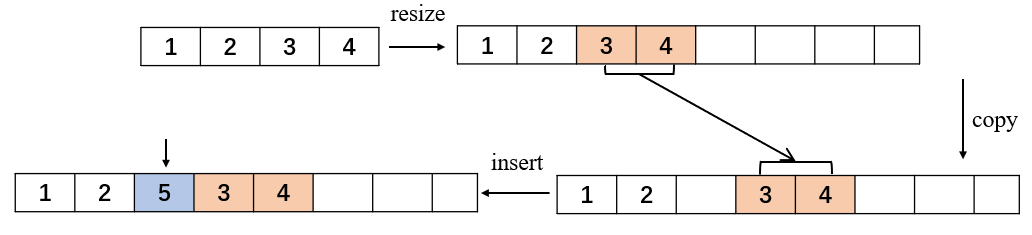
下面以在索引index=2，元素未5为例： 主要分为有无扩容的请况
1）增加元素-未扩容：
- 复制元素向后移动
- 插入元素到索引位置
程序实现：
public void add(int index, E e) {
if (size == data.length)
resize(2 * data.length); //开辟新空间
if (index < 0 || index > size)
throw new IllegalArgumentException("addLast failed, Required index < 0 || index > size");
System.arraycopy(data, index, data, index + 1, size - index); // 向后移动一位
data[index] = e; // 增加元素
size ++; // 维护size
}
// 私有函数 开辟新空间
private void resize(int newCapacity) {
E[] newData = (E[]) new Object[newCapacity];
System.arraycopy(data, 0, newData, 0, size); // 复制数组数据到新数组
data = newData;
}增加元素对应扩容，那么删除元素对应缩容，当删除元素后 size < capacity / 2的时候进行缩容。否则直接让对应位置等于 null 即可。
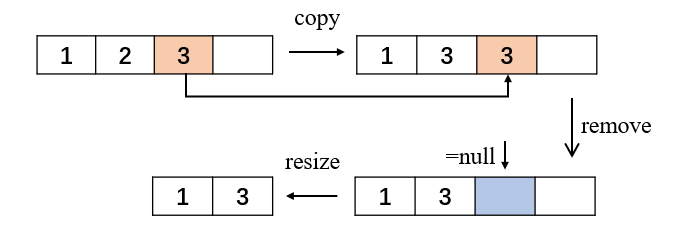
下面以删除索引为1的元素为例 ： 主要分为有无缩容的请况
1）删除元素-未缩容的情况 ：
- 将要删除元素后面的数据向前移一位
- 删除数据中最后一位的元素，索引为size(删除后size已经减 1)
- 将要删除元素后面的数据向前移一位
- 删除数据中最后一位的元素，索引为size(删除后size已经减 1)
- 进行缩容，将原数据复制到原数组大小一半的新数组中
下面以set(2, 5)为例 ：
查找元素分为三种，查找是否有这个元素，查找这个元素所在位置，根据索引返回元素这三种。 查找是否有这个元素和查找这个元素所在位置代码实现相似，一个找到了返回 true,一个找到了返回 index。 1）查找是否有这个元素
public boolean contains(E e){
for (int i = 0; i < size; i++) {
if (data[i].equals(e))
return true;
}
return false;
}2）查找这个元素所在位置
public int find(E e) {
for (int i = 0; i < size; i++) {
if (data[i].equals(e))
return i;
}
return -1;
}1）增加元素的复杂度 最好的情况是向最后的位置添加元素复杂度为 O(1) ，最坏的情况是向头添加元素，因为需要数据整体向后移动,复杂度为 O(N) ，根据均摊复杂度得出复杂度为 O(N/2) = O(N)，也就是说增加元素的复杂度为 O(N)。但是这仅仅是考虑没有扩容的情况产生。但是对于扩容的也是遍历一边数组进行复制的操作，所以复杂度也为 O(N)。 综上所述增加操作的时间复杂度为 O(N)
| 方法 | 复杂度 |
|---|---|
| addFirst(e) | O(1) |
| addLast(e) | O(N) |
| add(index, e) | O(N/2) = O(N) |
| resize(newCapacity) | O(N) |
2）删除元素的复杂度 删除元素的时间复杂度同增加元素完全相同。一个扩容一个缩容，实现机理相似。也就是说删除操作的时间复杂度也是 O(N) 级别。
| 方法 | 复杂度 |
|---|---|
| removeFirst() | O(1) |
| removeLast() | O(N) |
| remove(index) | O(N/2) = O(N) |
| resize(newCapacity) | O(N) |
3）修改元素复杂度 修改操作利用了数组的优势，支持随机访问。也就是可以在 O(1)的复杂度的情况下完成操作。
| 方法 | 复杂度 |
|---|---|
| set(index, e) | O(1) |
3）修改元素复杂度 修改操作对应三种情况，对于支持索引查找的get方法复杂为 O(1)。对于contain方法和find方法两者类似，需要遍历数组，最好的情况是在最开始就找到想要查找元素，最坏的情况是想要查找的元素在末尾，根据均摊复杂度，两者的复杂度为 O(N)。
| 方法 | 复杂度 |
|---|---|
| get(index) | O(1) |
| contain(e) | O(N) |
| find(e) | O(N) |
对于时间复杂度的震荡发生在扩容和缩容的边界。addLast()导致扩容，removeLast()导致缩容，在边界反复添加和删除操作会导致时间复杂度震荡。导致时间复杂度一直维持在O(N)级别。
public E remove(int index) {
if (index < 0 || index >= size) {
throw new IllegalArgumentException("delete failed, Required index < 0 || index >= size");
}
E temp = data[index];
System.arraycopy(data, index+1, data, index, size-index-1);
size--;
data[size] = null;
if (size == data.length / 4 && data.length / 2 != 0) //解决复杂度震荡问题
resize(data.length / 2);
return temp;
}getSize() //获取数组大小
getCapacity() //获取数组容器
isEmpty() //判断是否为空
addFirst(E e) // 向数组头添加元素
addLast(E e) //向数组后添加元素
add(int index, E e) //向index索引处增加元素
get(int index) // 获取索引index处元素
set(int index, E e) // 修改索引index处为e
remove(int index) // 删除元素,返回删除的元素
removeFirst() //删除第一个元素,
removeLast() //删除最后一个元素
removeElement(E e) //删除某一个元素
removeAllElement(E e) //删除所有元素e
contains(E e) //判断数组是否包含元素e
find(E e) // 查找元素e所在位置
toString() //打印函数resize() //重新定义数组大小更多精彩内容欢迎大家关注我的微信公众号：TeaUrn
如果有问题或者疑问可以私信我或者微信上私信我。
也欢迎大家来我的主页: 曲怪曲怪 我在这里等你哦~~