[TOC]
优先队列也是一种队列,它的接口函数和队列相同。
public interface Queue<E> {
int getSize();
boolean isEmpty();
E dequeue();
void enqueue(E e);
E getFront();
}虽然代码相同,需要注意的是,出队操作:拿出最大值(优先级最高)。但相对于普通的队列有着宏观上的不同。
- 普通队列:先进先出,后进后出
- 优先队列:出队和入队得顺序无关,和优先级有关
形象地理解就是超市和医院的排队。超市排队这种特性就符合普通队列的形式。先排队先结账。医院就不一样啦,医院要优先处理急诊的病人,这就跟优先级有关,优先级越高的元素放在最前面。优先进行处理。
不同的底层实现方法:
作为一种抽象的数据结构,底层实现的方法包含很多。数组或者链表这种线性结构,当然还有我们的树结构,当然我们也可以引入顺序的线性结构。具体的复杂度如下:
| 入队 | 出队 | |
|---|---|---|
| 普通线性结构 | O(1) | O(N):拿出最大元素 |
| 顺序线性结构 | O(N):顺序放入元素 | O(1) |
| 二叉堆 | O(log(N)) | O(log(N)) |
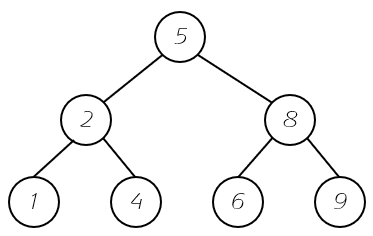
二叉堆是一个完全二叉树。那什么是完全二叉树呢? 满二叉树就是除了最下面一层,其他的节点都是具有左右孩子节点,就类似于这样。
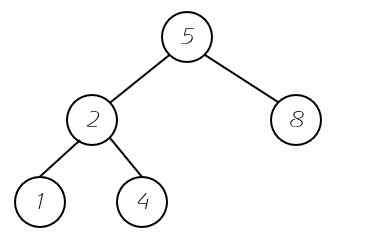
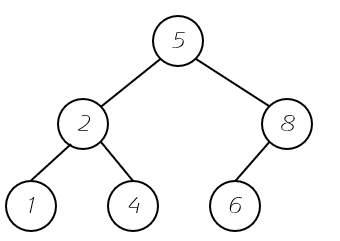
完全二叉树就类似这种:
完全二叉树不是一颗满的二叉树,但是它的不满的那一部分一定在他的右下角部分。存放的过程也就是从左向右的过程。
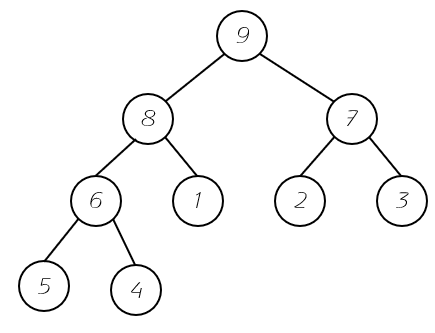
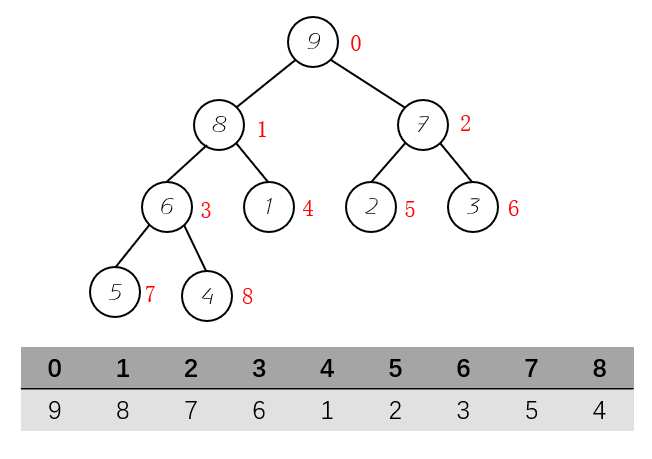
堆的特性和二分搜索树不同,堆的某个节点总是不大于其父亲节点的值。也就是它并不具有顺序性。我们可以看一下下面这张图。
可以看出任意子树的最大值永远是自己的父亲节点。
这里我们可以看出来二叉堆是一层一层的从左到右这么依次排列的,所以这里我们使用数组进行存储二叉树。通过数组索引找到节点。
这样我们就非常巧妙的将树结构存储到了数组当中。我们还可以发现下面的规则:
- 左孩子的索引等于该父亲节点索引值的 2 倍 + 1
- 有孩子的索引等于该父亲节点的索引值的 2 倍 + 2
- 父亲节点的索引值等于左右孩子节点的(索引值 - 1) / 2
用代码展示就是:
parent(i) = (i - 1)/ 2;//获得i索引值的父亲节点索引值
leftChild(i) = i * 2 + 1
rightChild(i) = i * 2 + 2在最大堆这个数据结构当中我们使用的是数组的底层实现,当然我们也就需要动态数组来实现这个动态大小的最大堆。关于Array动态数组这一章可以参考Array 动态数组。当然也可以直接使用Java自带的动态数组。
初始化程序实现:
public MaxHeap() {
data = new Array<>();
}
public MaxHeap(int capacity) {
data = new Array<>(capacity);
}节点索引查询实现: 我们需要对查询父亲节点进行判断,因为index-1操作会导致负值出现。
private int parent(int index) {
if (index == 0)
throw new IllegalArgumentException("index isn't zero");
return (index - 1) / 2;
}
private int leftChild(int index) {
return index * 2 + 1;
}
private int rightChild(int index) {
return index * 2 + 2;
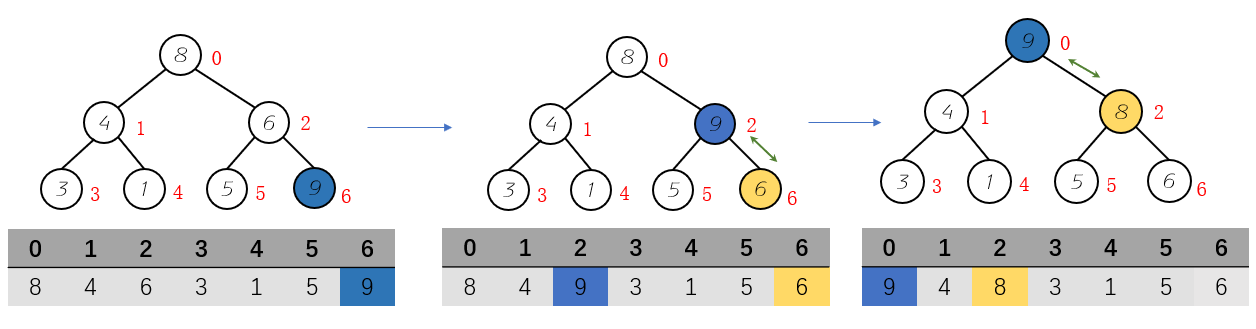
}这里的操作底层实现其实是上浮(SiftUp)操作。下面我们就来看看是如何上浮的。
- 向数组末尾添加一个元素,也就是向树的最下角添加一个元素;
- 根据堆的性质,父亲节点大于它的左右孩子节点,来进行替换操作
- 不断进行第二步操作直到待添加节点小于它的父亲节点
程序实现:
public void add(E e) {
data.addLast(e);
siftUp(data.getSize() - 1);
}
private void siftUp(int index) {
while (index > 0 && data.get(parent(index)).compareTo(data.get(index)) < 0) {
data.swap(parent(index), index);
index = (index - 1) / 2; //父亲节点也就是待插入元素现在的位置
}
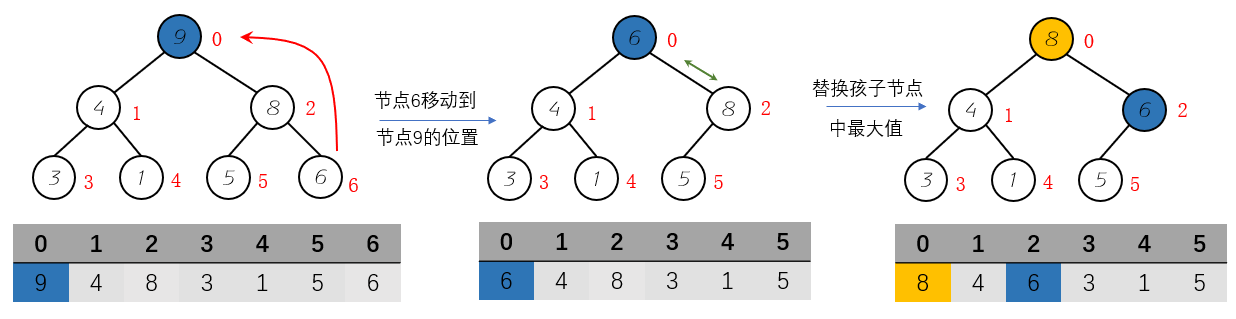
}对于我们上面实现的最大堆,看得出来,最大值的地方存在于根节点的位置。也就是数组索引位0的位置。而且我们需要维护二叉堆的性质。 步骤:
- 用树最后一个节点移动到根节点
- 判断待下沉操作的节点必须大于孩子节点的最大值,如果大于那么循环结束,否则替换孩子节点最大值和待下沉节点的位置。
提取最大值程序实现:
public E extractMax() {
E ret = findMax(); //查找最大值
data.swap(0, size() - 1); //移动最后一个节点到根节点
data.removeLast();
siftDown(0);
return ret;
}
// 下沉操作
private void siftDown(int index) {
while (leftChild(index) < size()) {
int j = leftChild(index);
if (j + 1 < data.getSize() && data.get(j + 1).compareTo(data.get(j)) > 0)
j++; //右孩子节点值大
if (data.get(index).compareTo(data.get(j)) >= 0)
break;
else
data.swap(index, j);
index = j;
}
}查询操作就是查找元素最大的值,这里就是根节点位置,也就是索引为 0 的位置。 程序实现:
public E findMax() {
if (isEmpty())
throw new IllegalArgumentException("Empty");
return data.get(0);
}replace替换操作主要包括:去除最大元素,放入一个新的元素。这其实是一个组合操作。但这里我们准备封装一下,并对其进行优化。
优化的方式就是在删除元素这里,如果我们分extraMax和add操作就需要两次 O(log(N)) 级别的时间复杂度。在replace操作中,我们可以直接将待添加的元素元素替换到根节点的位置,然后在执行下沉操作就可以,这样就是一次 O(log(N)) 级别的时间复杂度。
程序实现:
public E replace(E e) {
E ret = findMax();
data.set(0, e);
siftDown(0);
return ret;
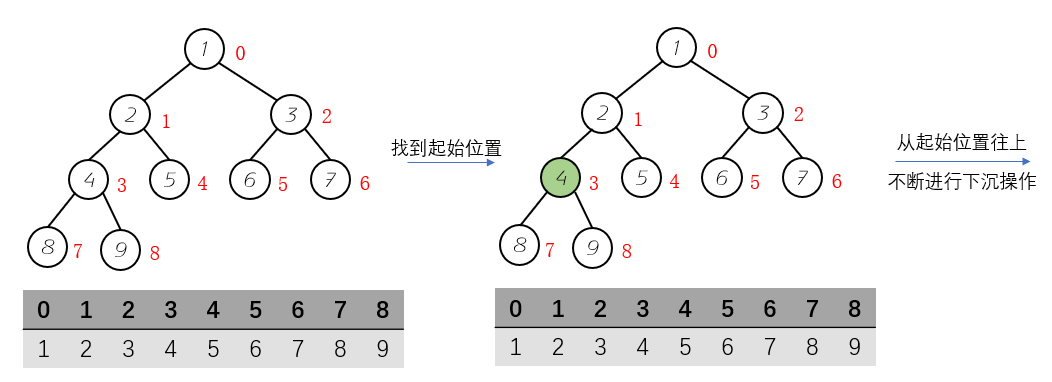
}操作就是将任意数组整理成堆的形状。 具体的过程就是:
- 找到树结构的倒数第一个非叶子节点;
- 不断向上进行下沉SiftDown操作
初始位置的查询就是最后一个节点的父亲节点。
程序实现:
public MaxHeap(E[] arr) {
data = new Array<>(arr);
for (int i = parent(arr.length - 1); i >= 0; i--)
siftDown(i);
}具体的函数方法其实在最大堆已经映射过了。
| 优先队列 | 最大堆 | |
|---|---|---|
| 入队操作 | enqueue | add |
| 出队操作 | dequeue | extraMax |
| 查询栈顶元素 | getFront | findMax |
@Override
public E dequeue() {
return maxHeap.extractMax();
}
@Override
public void enqueue(E e) {
maxHeap.add(e);
}
@Override
public E getFront() {
return maxHeap.findMax();
}更多精彩内容,大家可以转到我的主页:曲怪曲怪的主页
或者关注我的微信公众号:TeaUrn
或者扫描下方二维码进行关注。里面有惊喜等你哦。
源码地址:可在公众号内回复 数据结构与算法源码 即可获得。