Como en cualquier otra ciencia, la ciencia de datos depende de experimentos para comprobar hipótesis y validar/rechazar suposiciones sobre un fenómeno particular. Es por esto, que saber diseñar experimentos es una de las habilidades más importantes de la estadística y consecuentemente de la ciencia de datos.
En eset ReadMe encontrarás el concepto teórico y en el Notebook, una aplicación del diseño de experimentos al famoso data set de avistamientos OVNI.
Si tienes alguna pregunta, no dudes en contactarme en Twitter: @XaviGrowth
La diferencia entre observaciones y experimentos es muy importante en estadística, por lo cual tiene un impacto importante en Data Science. Sin importar si usamos datos observacionales o experimentales, las conclusiones pueden variar según como diseños un experimento.
Supongamos que conoces a un grupo de boomers (nacidos entre 1960 y 1975) que gustan de escuchar a The Rolling Stones. ¿Sería correcto asumir que toda la generación boomer es fanática de The Rolling Stones? Por supuesto que no, porque aunque los boomers comparten muchas características generacionales no podemos asumir que sus gustos son idénticos.
En este caso, para llegar a conclusiones más solidas tenemos que diseñar un experimento que observe a la población en su totalidad. Digamos que hacemos un experimento en donde hablamos con 100 boomers de nuestra ciudad. De ellos, a 91% les gustan The Rolling Stones. ¿Podríamos decir que este es un experimento bien diseñado? Nuevamente no. En este caso, aunque mejor que en el primer experimento, no podemos dibujar conclusiones ya que 100 boomers de nuestra ciudad sigue siendo un número muy pequeño para representar a todos los boomers del mundo y solo hemos entrevistado a personas locales.
Es en estos casos que debemos hacer una distinción entre observaciones y experimentos.
Una observación es el registro de un valor particular en un punto de tiempo determinado. Por ejemplo, un valor cuantititativo como cuanto medías a los 10 años o un valor cualitativo como tu sabor favorito de helado. En un estudio observacional colectamos muchas observaciones que consideramos importantes. Sin embargo,no podemos cambiar nada sobre la situación o variables involucradas en el estudio.
En cambio, un experimento involucra la aplicación de tratamientos especiales para seleccionar grupos a lo que le sigue una observación de valores específicos. Los experimentos siempre involucran una manipulación directa o inderecta de la situación con el fin de encontrar una relación entre dos variables.
Por ejemplo, podríamos hacer un experimento que involucre dividir personas en dos grupos. Un grupo recibirá un cereal azucarado y el otro un cereal bajo en azúcar. Después podemos medir sus niveles de actividad por las siguientes horas. El experimento nos puede ayudar a identificar la relación entre la ingesta de azúcar y los niveles de actividad. En este caso, estaríamos alterando los niveles de las variables (cantidad de azucar consumida).
En este caso, hay que examinar el concepto de significancia estadística. Aquí no hacemos referencia a la importancia o diferencia en los resultados, sino a la posibilidad de que un resultado haya sido causado por aletoriedad.
Digamos que queremos saber si una moneda esta truqueada hacía resultar en cara cada vez que se tira. Si tiramos la moneda dos veces, el hecho de que en ambos casos haya salido cara no significa que en realidad la moneda este truqueada. Por ende, no podemos decir que sea estadisticademente significativo. Si tiraramos la moneda 100 veces y todas fueran cara, en ese caso hablaríamos de significancia estadística porque es muy poco probable que eso suceda.
El Teorema de Bayes nos señala que dado una Hipótesis H y evidencia E:
[La evidencia que H sea cierto dado que E sucedió] = [La probabilidad que suceda H] ⋅ [La probabilidad de que E sea cierto dado que H sea cierto] / [La probabilidad natural de E]
Matemáticamente ser vería así:
P(H|E) = P(H) ⋅ P(E|H) / P(E)
Consideremos el siguiente escenario: hay una extraña enfermedadq ue afecta al 1% de la población. Hay una prueba que detecta precisamente el 99% de los casos. Es decir, si tienes la enfermedad la detectará correctamente el 99% de veces y si no la tienes, no la detectará el 99% de las veces.
Si sales positiva/o en la prueba, que probabilida hay que la prueba este en lo correcto?
Veamos como sustituiriamos cada uno de los valores para calcular las probablidades:
P(Tener la enfermedad dado la prueba) = P(tener la posibilidad de dar positivo dado que tienes la enfermedad) ⋅ P(tener la enfermedad) / P(tener una prueba positiva)
P(D|T) = 0.99 ⋅ 0.01 / 0.0198
P(D|T) = 0.5
Por tanto, la posibilidad de tener la enfermedad es del 50%. Veámoslo así: de una población de 10,000, esperamos que 100 tengan la enfermedad y 9,900 no. De los 100 que tienen la enfermedad, 99 darán positivo. De los 9,900 que dan negativo, el 1% (99) tienen la enfermedad. Por tanto, en total 198 tienen la enfermedad.
El objetivo de diseñar experimentos es controlar sesgos tanto como sea posible. Esto se puede hacer bloqueando unidades experimentales o controlando factores aleatoreos en un escenario. El objetivo es crear un experimento donde la única diference entre las unidades experimentales sea el tratamiendo que nos interesa.
Digamos que queremos estudiar las estaturas de los estudiantes en una escuela. Sería un error utilizar los datos del equipo escolar de basquetbol porque podemos asumir que no son representativos al ser los estudiantes más altos. Una buena muestra puede incluir algunos jugadores de basquetbol, pero incluirlos exclusivamente crearía un sesgo. El resultado sería un promedio alto y poca desviación estándard en comparación si utilizaramos una muestra más representativa.
Sin embargo, no todos los sesgos son obvios. Tomemos las encuestas telefónicas hechas con números que son públicos. En este caso, los teléfonos fijos estarían más presentes y (presumiblemente) los contactos pertenecerían a personas de mayor edad. Por otra parte, las encuestas de producto tienden a ser respondidas por personas que tienen opiniones fuertes al respecto.
Dado que es impráctico (y muchas veces imposible) medir los intereses individuales de cada cliente, el objetivo de nuestro diseño de experimentos es asegurar que las muestras sean representativas de la población de interés. La estrategia más sencilla es implementar un muestro simple aleatorio en donde el grupo de estudio es elegido al azar. Sin embargo, este enfoque puede no siempre ser el mejor.
Supongamos el siguiente escenario: queremos entrevistar a pasajeros de una aerolínea sobre el servicio que recibieron a bordo. Si tomaramos un día, hora, y terminal al azar ¿Sería esta un método que produzca una muestra representativa? Para esto, hay que tomar en cuenta algunos detalles:
- Los pasajeros que viajan por negocios viajan frecuentemente entre semana y los turitas en fin de semana.
- Los pasajeros llegando en la mañana podrían haber viajado durante la noche.
- Un mal clima puede afectar la experiencia del cliente (piensa en turbulencias), por lo que podría afectar el resultado en comparasión a viajes durante buen clima.
Es decir, aún si se toma un día, hora y terminal al azar puede haber un sesgo ya que los pasajeros en dichos vuelos tendrían algo en común. Por ende, tomar una muestra aleatoria no es suficiente para un experimente exitoso.
El doble ciego es una herramienta con la que podemos reducir el sesgo en nuestro estudios experimentales. Este método es usado ampliamente en la industria médica, en la que las personas que piensan recibir un médicamente pueden sufrir de un efecto placebo. Se considera que un estudio tiene doble ciego cuando los participantes e investigadores desconocen que tipo de tratamiento o intervención están recibiendo (de ahí el nombre). La razón por la que los investigadores suelen también desconocer el tipo de tratamiento es porque:
- Previene que los investigadores comuniquen por error información que afecte el resultado.
- Previene la manipulación de resultados hacia un resultado deseado.
- Hace más difícil que los investigadores cambien intencionalmente los resultado.
Aún así, hay maneras de contaminar nuestra data de forma accidental. Previamente hemos visto como una muestra mal seleccionada puede generar resultados fallidos. Otra estrategia a tomar en cuenta son las variables de confusión. Esto sucede cuando nuestro estudio esta ligado con otro efecto o influencia. Cuando una confusión sucede, perdemos la habilidad de distinguir entre los efectos de un tratamiento y las influencias de dicha confusión. Si la confusión es severa, los resultados de nuestro experimento pueden ser completamente invalidados.
Un caso de estudio se dio en la Universidad de Cornell. Un profesor quiso saber que tanto su tono de voz afectaba a sus estudiantes. El profesor enseñó la misma clase en dos semestres diferentes y con estudiantes diferentes. El curso fue idéntico, a excepción de que su tono de voz era más entusiasta en el segundo semestre. Las clasificaciones de los estudiantes fueron las mismas en ambos semestres. Sin embargo, la evaluación de curso mejoró de forma importante en el segundo semestre.
La conclusión fue que la "varación en el tono de voz del profesor tuvo un efecto importante en la evaluación dada por los estudiantes". Sucede que, empero no hay forma de saber que tanto este cambio se dio gracias al profesor. El cambio se pudo dar por otros factores:
- El humor de los estudiantes puede cambiar de invierno a verano.
- La presión debido a otras clases.
- El tipo de estudiantes que tomaron la clase en cada uno de esos semestres.
Este experimento se contaminó con variables de confusión, por lo que no podemos separar los efectos y como contribuyó cada uno al resultado final.
Cuando diseñamos un experimento, hay muchos factores en la muestra que debemos de considerar: tamaño, conveniencia y aleatoriedad. Miremos los siguientes ejemplos:
- Supongamos que queremos saber la eficiencia de un fertilizante nuevo, midiendo que tanto contribuye al crecimiento de las plantas y queremos medirlo en dos tipos de plantas: chicharos y tulipanes. La fomra correcta de realizar el experimento sería separar los tipos de plantas y asignar tratamientos aleatoriamente dado que al ser diferentes plantas podrían ser afectados de forma diferente por el fertilizante.
- Supongamos que queremos saber cuantas horas de estudio invierte cada estudiante para prepararse para un examen. En este caso, sería inteligente dividirlos en el grado académico en el que están ya que podemos asumir que las horas de estudio son proporcionales al año de estudio.
A estas estrategías las conocemos como blocking. Con esto podemos recudir el impacto de confundir variables en nuestros experimetnos al separarlos en grupos de sujetos. Soleemos utilizar esta técnica cuando sospechamos que tenemos una razón para creer que nuestros sujetos difieren en cierta forma que influencía nuestras medidas o cuando creemos que nuestro tratamiento puede afectar a diferentes grupos de sujetos diferentes.
Usando blocking podemos reducir el tamaño de cada experimento, dado que cada grupo se considerará individualmente. En el caso de los fertilizantes, lo podemos visualizar así:
Aunque el muestro simple aleatorio es la forma más fácil de obtener una muestra de una población, una mejor estrategia es el muestro estratíficado. Con este dividimos primero a nuestra población en grupos para luego tomar de forma aleatoria y proporcional la muestra en cada grupo.
Volviendo al ejemplo de las horas de estudio, si nuestros estudiantes de 1er grado son 600, de 2do son 500, de 3ro son 500 y de 4to son 400, nuestro experimento debería de tomar una muestra donde la estratificación sería del 30%, 25%, 25% y 20% respectivamente.
Un método común en el diseño de exprimento es el muestreo por conglomerados. En este caso, tomamos un grupo pequeño que pensamos podría ser representativo de toda la población. Sin embargo y aunque el muestreo por conglomerados puede ser representativo, esto último no se puede asegurar en todos los casos. Aunque es fácil de obtener, puede también tener sesgos.
Otra posible solución es el muestreo sistemático, en donde escogemos un intervalo que viene de una lista que contienen a la población. En este caso nos queremos asegurar que la posición de inicio sea aleatoria. De lo contrario, podemos correr el riesgo de tener el un sesgo. En el caso del servicio al cliente en una aerolínea. Si tomásemos el primer o último vuelo como referencia (en vez de cualquier vuelo aleatorio) podríamos siempre o nunca medir a los mismo usuarios.
Por tanto queremos asegurarnos que nuestra muestra incluya lo más posible de la lista. De la misma manera, es importante asegurarnos que el orden de la lista no este relacionado con lo que intentamos medir. Si tal orden no existe, tomar una posición cualquiera haría de dicha muestra completamente aleatoria. Con muestreo aleatorio mitigamos el riesgo de un sesgo de forma efectiva. En el caso de los vuelos, sería mejor ordenarlos por número de vuelo que por hora de llegada.
Hay ocasiones cuando la varianza entre las variables es tan significativa que vale la pena hacer sentido de las diferencia entre sujetos de muestra en vez de tomar muestras aleatorias.
Supongamos que tenemos la hipótesis que ganar un lanzamiento de moneda beneficia al que lo gana en un partido de fútbol americano. Medir la diferencia en puntos anotados entre ganadores y perdedores sería la mejor estrategia para comprobar nuestra hipótesis. Dado que sospechamos que el número de puntos anotados varia significativamente en cada partido y que los juegos vienen en pares (ganador y perdedor del lanzamiento de moneda), tiene sentido calcular las diferencias entre estos. A esto le llamamos muestras de ajuste.
Si miramos a los resultados de los Super Bowls, veremos que en los primeros 52 juegos el promedio de las diferencias (que tantos puntos de diferencia anotó el equipo que ganó le lanzamiento de moneda) es de +1.21. Por tanto, esta hipótesis es ligeramente cierta. No hay que olvidar que la varianza en este caso es grande. La desviación estándard es de 17.7 puntos, lo que es considerables dentro de un partido de fútbol americano. Si queremos saber si esta hipótesis es cierta, deberíamos obtener aún más datos.
Si seguimos los planteamientos del Teorema del Límite Central, sabremos que en la mayoría de casos las muestras producen valores normalmente distribuidas alrededor de los valores reales de la población. Es decir, una muestra que en verdad es aleatoria debaría de estar localizada mayormente en el 95% de la distribución. Si tomaramos un valor aleatorio de la muestra y señalaramos que ese valor es positivo en un 10 a 12% de los casos, generaríamos un rango que contiene ese valor y al que conocemos como el intervalo de confianza.
Supongamos que tomamos a 1,000 personas en una ciudad, de las cuales el 3.1% hablan alemán siendo que el censo del gobierno apunta a que solo el 2.6% de los habitantes hablan ese idioma. Dada esta información, podemos concluir que el valor real de hablantes de alemán es del 3.1% aunque no podemos tener seguridad total al respecto. No debemos de olvidar que aunque nuestro muestreo haya sido excelente, nunca podemos estar seguros del valor real. Para saber que tanto el valor real está de nuestras estimaciones, usamos el conepto de intervalos de confianza.
En este caso diríamos que hay un 95% de probabilidades que el número de hablantes de alemán está entre el 2.0% y el 4.2%. Esto lo podemos saber ya que utilizamos el error estándard. Este se calcula con la siguiente fórmula:
√[Proporción] ⋅ [Propoción - [1 - Proporción]] / Número de Individuos en la Muestra
Digamos que con una muestra de 900 árboles en un bosque, encontramos que 280 son de maple. El cáluclo sería así:
√[280/900 ≈ .3111] ⋅ [1 - .3111 ≈ .6889] / 900
≈ 0.015 = 1.5%
Hay que tomar en cuenta que aunque los intervalos de confianza son herramientas útiles, en 5% de los casos el valor real se encuentra fuera de este rango. Es decir, en 1 de cada 20 casos.
Cuando llegamos a pruebas de hipótesis tenemos una teoría sobre el mundo y como se ven nuestros datos recolectados. En este punto queremos saber si nuestra teoría es correcta o no. En este caso tenemos una o varias teorías. Algunas teorías podrían ser:
- Masticar chicle puede causar piedras en el riñón.
- El boxeo provoca daños al tejido cerebral.
La recolección de datos nos permite validar (o no) estas teorías. En cualquier experimento, debemos de considerar la posibilidad de que nuestra teoría esté equivocada. A esto lo conocemos como hipótesis nula y la denotamos como H0. Las hipótesis nulas son de utilidad como un modelo para considerar la posibilidad de que nuestros datos pudieran ser explicado por aletoriedad. Por ejemplo, con una H0 podemos simplificar que mascar chicle no es un riesgo para desarrollar piedras de riñón.
Por ejemplo, una empresa financiera utiliza un algoritmo de machine learning para detectar fraudes. En promoedio falla el 5% de casos al día. Después de una actualización, el algoritmo solo falla en promedio 3.5% al dia. Para aplicar una hipótesis nula, deberíamos preguntarnos: ¿Qué posibilidad hay de ver esos mismos resultados si el promedio fuera el 5%? En este caso, simplemente ponemos en duda que el promedio de fallos del algoritmo sea del 5% y estaríamos aplicando una H0.
Para usar correctamente un modelo normal, es importante que nuestro data set tenga suficientes data points. Una regla general es que para que nuestros resultados puedan ser calculados como éxito o fracaso, nuestra muestra debe ser lo suficientemente grande como para que tengamos 10 ocurrencias tanto de éxito como de fracaso.
Regresando al algoritmo para detectar fraudes, supongamos que el porcentaje de fallos baja hasta el 0.8%. El número de muestras para considerar que una prueba sería exitosa es de 1,250. Dado que esperamos que el algoritmo falle en 0.8% de los casos y queremos que haya tanto 10 éxitos como 10 fracasos, nuestra operación sería la siguiente:
10 / 0.008 = 1250
Si hicieramos 100 pruebas con el agoritmo y tuvieramos 99 éxitos y 1 un fallo, podríamos determinar que el margen de error es del 1%, dado que:
√(0.99)(0.01)/100 ≈ 0.00995
En este último caso, hemos calculado la desviación estándard para un modelo basado en una H0 en donde la proporción es igual a 0.99.
Con esto podemos usar un modelo normal basado en una hipótesis nula para calcular el valor p. El valor p nos da la probabilidad de encontrar el dato si la H0 es verdadera. Por tanto, el valor de 0.05 (por ejemplo) significaría que H0 sería cierta en 5% de los datos:
En la imagen anterior, esperaríamos encontrar los resultados un 5% de las veces en la zona roja dado que los resultados están a 2 o más desviaciones estándard de la media. A esto nos refeririamos como un valor p de 0.05.
Si el valor p es bajo, tenemos razones para pensar que la H0 es falsa. Es decir, el valor p nos puede mostrar que tanto nuestra hipótesis es cierta o falsa. en este caso usamos un valor p de 0.05 porque es un estándard en estadística para rechazar una hipótesis nula. Sin embargo, este no deja de ser un parámetro arbitrario y se debe de tomar con un grano de sal.
Digamos que según un reporte gubernamental, el coche más eficiente del mercado puede recorrer entre 4.6 y 5 kilómetros por litro de gasolina (k/l). Las medidas de tendencia central en una muestra de 325 coches nos indican que:
- La media es 4.5 k/l.
- La mediana es 4.5 k/l.
- La varianza es 3.2 k/l.
- La desviación estándard es 0.56 k/l
- El estimado de la desviación estándard de la población es de 0.56%
En este caso queremos saber si el reporte está en lo correcto. De entrada, vemos que la media está fuera del rango dado por el gobierno por lo que tenemos que investigar más a fondo. Por tanto, nuestra H0 es que el valor de μ es igual o mayor a 46.
Podemos entonces modelar la desviación estándard de la población usando las desviaciones estándard de nuestra muestra. Al no saber el promedio de la población, usaremos el promedio de la muestra. Esto requiere que usemos grados de libertar para corregir el sesgo de nuestra muestra. Por tanto, calculamos que s = 0.5678.
Entonces, el error estándard es:
0.5678 / √325 = 0.0315
Basado en este error, si el promedio de la población es 4.6 esperaríamos que nuestra muestra caiga por debajo de 4.6 en 50% de los casos, debajo de 4.6 - 0.0325 = 4.5685 en 15.9% de los casos, debajo de 4,6 - 0.2(0.0315) = 4.537 en 2.3% de los casos y así sucesivamente.
Calculamos el z-score de nuestra muestra como 4.5, lo que haría que z fuera:
4.5665 - 4.6 / 0.0315 ≈ −1.063
lo que es solo un poco más que una desviación estándard por debajo de la H0 de 46. Si el promedio es de 4,6, esperaríamos que el 14.4% de las muestras recolectadas se vieran así. Por tanto, no tenemos evidenvia para decir que el reporte esté equivocado.
Cuando trabajamos con datos experimentales, siempre hay un número de aletoriedad e incertidumbre en nuestros datos. Por ende, es de ayuda pensar sobre que tipos de errores se hacen.
En las pruebas de hipótesis, tenemos una teoría que queremos probar y compararla con la H0. En este sentido, hay dos tipos de errores:
- Tipo I: la H0 es verdadera, pero la rechazamos (falso positivo).
- Tipo II: la H0 es falsa, pero la aceptamos (falso negativo).
Digamos que tenemos una H0 tiene un valor p de 0.05 o menor. Al rechazarlo tendríamos un falso positivo en 5% de los casos. En este caso, estamos aceptando la evidencia como válida en nuestra hipótesis alternativa. Sin embargo, como tenemos un valor p de 0.05 hemos aceptado que este resultado sucederá el 5% de las ocasiones debido a que la variación en las muestras aún si la H0 es cierta. En este caso, caemos en un error de Tipo I.
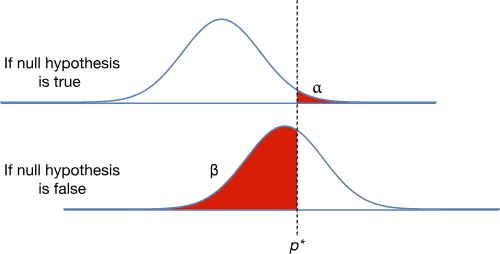
En el siguiente diagrama, podemos notar una línea que representa el borde del valor p. Esta es una propción particular en la que tenemos que encontrar para rechazar la H0. Si nuestro experimento produce un valor por encima de p*, debemos de rechazar la H0. Se encontramos un valor por debajo de H0, no debemos de rechazar la H0. En este caso, los errores están marcados en rojo. El primer gráfico es un error de Tipo I y el segundo un error de Tipo II.
Todo esto tiene implicaciones importantes en la vida real. Digamos que queremos crear un sistema de detección de enfermedades. En este caso, queremos reducir la cantidad de falsos positivos. Es decir, queremos poder detectar enfermedades la mayoría de las veces. Por ende, será imortante tener un valor p elevado dado que esté es la posibilidad de un falso positivo. Como queremos reducir la probabilidad de un falso positivo, necesitamos incrementar el valor p.
Veamos que un valor p elevado significa que hay una mayor probabilidad de que salga un resultado positivo de un grupo de variaciones aleatorias en un modelo de H0. Como queremos evitar falsos negativos, tenemos que usar un valor p mayor. Nuestro sistema se volvera más sensible y menos probable de descartar resutados reales. En consecuencia, tendremos más resultados positivos (tanto falsos como verdaderos).
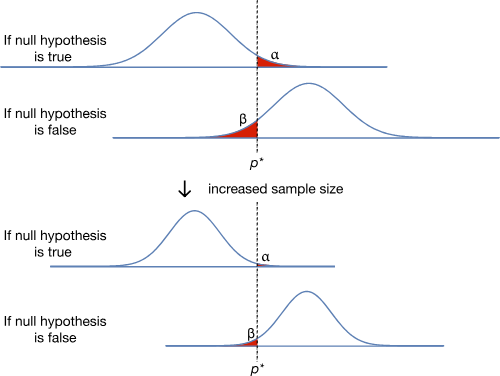
Si movieramos la línea de valores p, el diagrama cambia de la siguiente forma:
Al mover p* a la izquierda (aumentando el valor p) se reduce la probabilidad de un falso negativo, lo que aumenta la posibilidad de un falso positivo. Hay que notar que el p* representa la proporción crítica en el que deberíamos rechazar H0. Por tanto, cuando p* se mueve a la izquierda del valor p se incrementa.
Los errores de Tipo I se le conoce como α (alfa) y a los de Tipo II se le conoce como β (beta). Saber que probabilidad hay que modificar depende de cada caso. Calcular α tiende a ser más fácil que calcular β porque aunque podemos calcular cualquier valor específico de un hipótesis alternativa, no podemos saber con exactitud el efecto verdadero que tendá el experimento.
El poder del experimento es la probabilida de que seremos capaces de encontrar el efecto que estamos buscando. Si conocemos β, podemos calcular mejor dicho efecto dado que es el complemento de β. Es decir, 1 - β. Para experimentos con resultados pequeños, podemos colectar datos extensivamente para detectar resultados. De otra manera, el ancho de banda de nuestro experimento es muy pequeño.
El tamaño de la muestra, el valor de α y el tamaño del efecto son variables que afectan a β. El tamaño del experimento determina la distribución en la curva normal. Hay que notar como la hipótesis altera la gráfica si incrementamos el tamaño de la muestra:
Viendo los cambios de α dado los cambios de p*, vemos que β es afectado. La distancia entre H0 y la hipótesis alternativa también tiene un impacto. Hay que notar que tan grande β se hace cuando las proporciones están cerca una de la otra:
Así mismo, incrementar las posibilidades de un falso positivo hacen que nuestro experimento sea más poderoso.
Considerando el poder del complemento de β, al reducir el tamaño de la muestra e incrementar la posibilidad de una falso negativo (β) disminuye el poder de nuestro experimento.
Si incrementamos las posibilidades de un falso negativo (α), movemos p* a la izquierda lo que disminuye β y consecuentemente incrementaría el poder del experimento. Dicho de forma simple: una forma de hacer nuestro experimento más poderoso es apostar por obtener más falsos positivos.
Hay que tomar en cuenta que aunque no podemos reducir α y β reduciendo p*, es posible reducir a ambos. Cualquier cosa que reduzca la desviación estándard de nuestros datos reduce tanto α como β al mismo tiempo. El enfoque más común para lograr esto es incrementando el tamaño de la muestra:
Al cambiar el experimeto que reduce la desviación estándard, es posible reducir la probabilidad de ambos errores. Es por eso que los estudios más extensos suelen ser más significativos que los pequeños.
En resumen, todos los experimentos dependen de pruebas de hipótesis que es susceptible a dos tipos de errores.
- El error de tipo I (α) ocurre cuando rechazamos una H0 que es cierta.
- El error de tipo II (β) ocurre cuando no rechazamos una H0 cuando es falsa.
El poder del experimento es la probabilidad de encontrar resultados que son verdaderos y lo podemos describr como 1 - β.
Cada experimento debe seleccionar un balance apropiado entre probabilidades de estos dos errores y estas decisiones deben estar guiadas por reglas estadísitcas en vez de consideraciones del mundo real en donde los errores serán dados por circunstancias del ambiente.