7.4-level-averages-in-a-binary-tree-easy.md

7.4 Level Averages in a Binary Tree (easy)

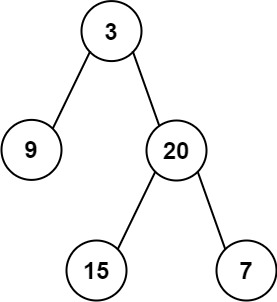
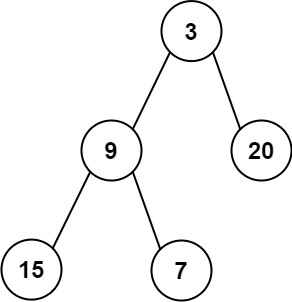
Given the root of a binary tree, return the average value of the nodes on each level in the form of an array. Answers within 10-5 of the actual answer will be accepted.

Example 1:

Input: root = [3,9,20,null,null,15,7]
Output: [3.00000,14.50000,11.00000]
Explanation: The average value of nodes on level 0 is 3, on level 1 is 14.5, and on level 2 is 11.
Hence return [3, 14.5, 11].

Example 2:

Input: root = [3,9,20,15,7]
Output: [3.00000,14.50000,11.00000]

Constraints:

• The number of nodes in the tree is in the range [1, 104].
• -231 <= Node.val <= 231 - 1

import java.util.*;

class TreeNode {
  int val;
  TreeNode left;
  TreeNode right;

  TreeNode(int x) {
    val = x;
  }
};

class Main {
  public static List<Double> findLevelAverages(TreeNode root) {
    List<Double> result = new ArrayList<>();
    if(root == null) return result;

    Queue<TreeNode> queue = new LinkedList<>();
    queue.offer(root);

    while(!queue.isEmpty()) {
      int levelSize = queue.size();
      double sum = 0;
      for(int i = 0; i < levelSize; i++) {
        TreeNode currNode = queue.poll();
        sum += (double)currNode.val;

        if(currNode.left != null) queue.offer(currNode.left);
        if(currNode.right != null) queue.offer(currNode.right);
      }
      result.add(sum/(double)levelSize);
    }
    return result;
  }

  public static void main(String[] args) {
    TreeNode root = new TreeNode(12);
    root.left = new TreeNode(7);
    root.right = new TreeNode(1);
    root.left.left = new TreeNode(9);
    root.left.right = new TreeNode(2);
    root.right.left = new TreeNode(10);
    root.right.right = new TreeNode(5);
    List<Double> result = Main.findLevelAverages(root);
    System.out.print("Level averages are: " + result);
  }
}

Time complexity #

The time complexity of the above algorithm is O(N), where ‘N’ is the total number of nodes in the tree. This is due to the fact that we traverse each node once.

Space complexity #

The space complexity of the above algorithm will be O(N) which is required for the queue. Since we can have a maximum of N/2 nodes at any level (this could happen only at the lowest level), therefore we will need O(N) space to store them in the queue.