BD-rate implementations in Matlab. Also available in Python.
The Bjøntegaard-Delta (BD) metrics (delta bit rate and delta PSNR) described in [1] are well known metrics to measure the average differences between two rate-distortion (RD) curves. They are based on cubic-spline interpolation (CSI) of the RD curves and Matlab as well as Python implementations are available on the internet.
However, this way of interpolation using a third-order polynomial leads to problems for certain RD curve constellations and causes very misleading results. This has also been experienced during the standardization of HEVC. Consequently, the so-called piecewise cubic hermite interpolation (PCHIP) has been implemented in the JCT-VC Common Test Conditions (CTC) Excel sheet [2] for performance evaluation. In further studies [4] - [5], it was found that Akima interpolation returns more accurate and stable results. An example for corresponding interpolated curves is shown below.
This page provides BD-rate implementations (see here for a Python implementation) for both PCHIP and Akima interpolation in Matlab. In our tests, the implementation of PCHIP returns the same value as the Excel-Implementation from [3] with an accuracy of at least 10 decimal positions. The scripts allow to calculate the BD for any number of RD points greater one.
Use the example_usage.m for testing.
Basic example with test data measured using ffmpeg (libx265 with different preset settings) and Akima interpolation:
# Test data
rate_anchor = [9487.76, 4593.60, 2486.44, 1358.24];
psnr_anchor = [ 40.037, 38.615, 36.845, 34.851];
rate_test = [9787.80, 4469.00, 2451.52, 1356.24];
psnr_test = [ 40.121, 38.651, 36.970, 34.987];
# Call calculation
bdr_akima = bd_akima(rate_anchor, psnr_anchor, rate_test, psnr_test);
disp(['Akima BDR: ' num2str(bdr_akima*100,'%4.16f') '%']);The parameters rate_anchor and dist_anchor describe the rate-distortion points of the anchor, rate_test and dist_test describe the rate-distortion points of the test codec.
Available interpolation methods:
'bd_pchip.m': Piecewise cubic hermite interpolation (used in standardizations [2], [3])'bd_akima.m': Akima interpolation [4]
For in-depth evaluation of codec comparison results, we recommend to take relative curve difference plots (RCD-plots) into account (see [5]). They can be created using:
bdr_akima = bd_akima(rate_anchor, psnr_anchor, rate_test, psnr_test, true);
Here is an example for a RCD plot.
The left plot shows the supporting points and the Akima-interpolated curves for both anchor and test. The right plot shows the relative horizontal difference between the two curves in percentage.
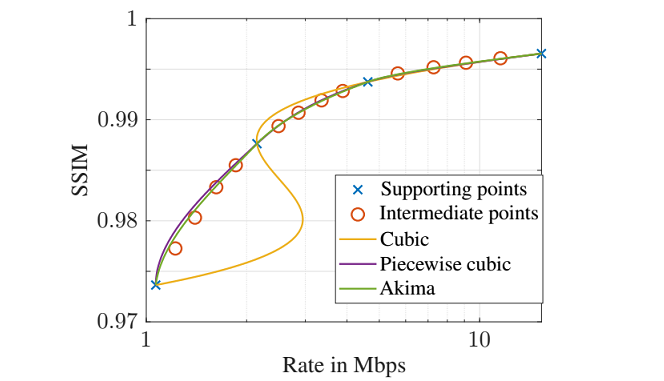
Furthermore, a comparison between the interpolated curves and intermediate, true rate-distortion points between the supporting points is shown in the plot below. For this example, the quality is represented by the SSIM value. Note that the example was cherry-picked to show that cubic interpolation can fail. The curve interpolated by the Akima interpolator is closest to the intermediate points.
[1] G. Bjontegaard, "Calculation of average PSNR differences between RD-curves", VCEG-M33, Austin, TX, USA, April 2001.
[2] F. Bossen, "Common HM test conditions and software reference configurations", JCTVC-L1100, Geneva, Switzerland, April 2013.
[3] F. Bossen, "VTM common test conditions and software reference configurations for SDR video", JVET-T2020, Teleconference, October 2020.
[4] C. Herglotz, M. Kränzler, R. Mons, A. Kaup, "Beyond Bjontegaard: Limits of Video Compression Performance Comparisons", Proc. International Conference on Image Processing (ICIP) 2022, online available.
[5] C. Herglotz, H. Och, A. Meyer, G. Ramasubbu, L. Eichermüller, M. Kränzler, F. Brand, K. Fischer, D. T. Nguyen, A. Regensky, and A. Kaup, “The Bjøntegaard Bible – Why Your Way of Comparing Video Codecs May Be Wrong,” IEEE Transactions on Image Processing, 2024, online available.
BSD 3-Clause. For details, see LICENSE.