Huffman Compressor

Huffman code is a particular type of optimal prefix code that is commonly used for lossless data compression. Huffman coding, an algorithm developed by David A. Huffman. As we know that systems store in ASCII format. Where each character is 1 byte or 8 bits i.e. 256 different characters are possible and are present. For compressing the data, all 8 bits is not a necessary instead each character can assigned to a number (which will be followed further steps). Based on the number assigned we compress the data.

Huffman Coding Example

Consider the text:

hello world he rolls

Total number of bits : 160 bits (or 20 bytes) The frequency of characters from above text is as follows:

Character	Frequency
d	1
s	1
w	1
h	2
e	2
r	2
o	3
space	3
l	5

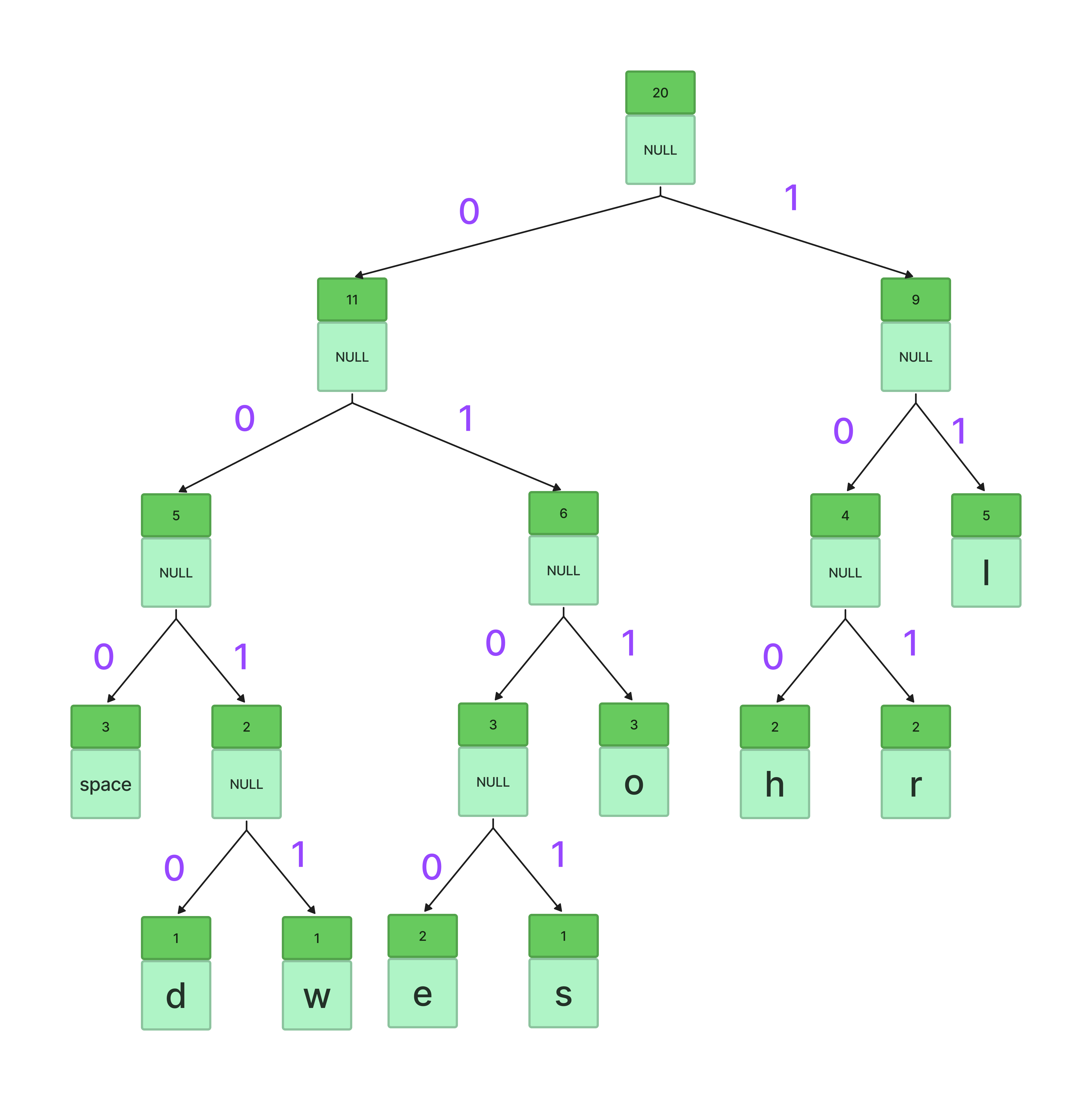
As frequency of character is known now, binary tree is created(will see in next section) and a binary value is assigned to each character:

Table

Character	Frequency	Value	Binary
d	1	2	0010
s	1	5	0101
w	1	3	0011
h	2	4	100
e	2	4	0100
r	2	5	101
o	3	3	011
space	3	0	000
l	5	3	11

Based on the binary value, we are going to compress the text: This is how it looks:

100010011110110000011011101110010000100010000010101111110101

Total number of bits : 60 bits (~8 bytes) Well it looks all in '1's and '0's, the fact is, it is in Binary.Compression ratio is around ~40%. This is how the compressed data looks. Usually along with this compressed text, the table is also shipped to the file. This is how Huffman encoding works. Characters with more frequency have less binary encoded digits and vice versa.

Huffman Encoding

Data Structure

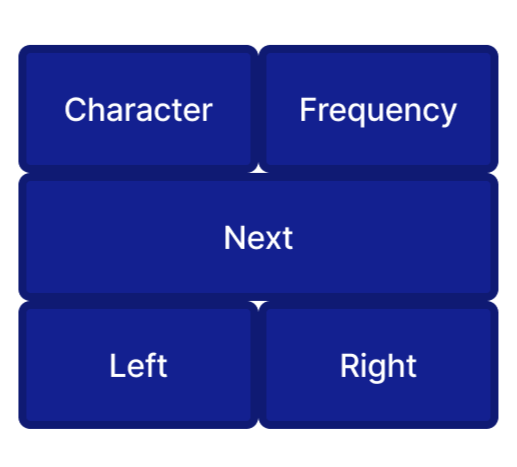
I have used a mixture of **Linked list** and **Binary Tree** data Structure. Above is a example node which contains *character* to store the characters present in the text, and *frequency* to store the number of repeatedly appearing characters. *Next* is a pointer used for **Linked list**, and *Left* and *Right* is used **Binary Tree**.

Method

Considering the sample example:

hello world he rolls

I created a linked list which looks like this:

Where the above box represents the frequency and below is the character. From the Linked list, Tree is created in such a way that, the two nodes are chosen with least frequency. the smallest frequency node comes to left and the greater one comes to right and a subtree is created. This process is done when there is no linked list nodes created. Just like the image below:

We can observe that the leaf nodes are the characters that is present in text(true for all text). Now, to encode each character with binary. We should encode in such a way that traversing to left is **left shifting once** (Example: 1 << 1 = 10 in binary) and traversing to right is **left shifting once and adding 1** (Example: (1 << 1) + 1 = 11 in binary). Similarly this is done to all characters. For character 'd' it is encoded as '0010' as so on. Then the table is imported. Hence the Compressed file is created.

Huffman Decoding

Method

For Decoding the compressed file, using the table I can recreate the original file. I do this by taking first 8 bits (or byte), compare the bits with the corresponding table, and print out to the file. I repeat this process unless all the bits are done. Interesting Fact : Binary Encoded Values are created in such a way that they do not overlap with other binary values. For example consider character 'h' = 100 and character 'e' = 0100, they both do not overlap each other (always consider taking from left).

Challenges Faced

1. The system cannot write data which is less than 8 bits(1 byte) which would lead to wastage of CPU cycles. So, To work around this I had to use 1 byte data type, so I used 'char' data type.
2. Considering the example, the compressed data is of 60 bits, which is not a multiple of 8, and left a remainder of 4. So, in this case the system would normally append the '0' into remaining places. I had to import the offset used to the compressed file.
3. I had to import the table to the compressed file, where I added at the beginning.

Sample File Compression

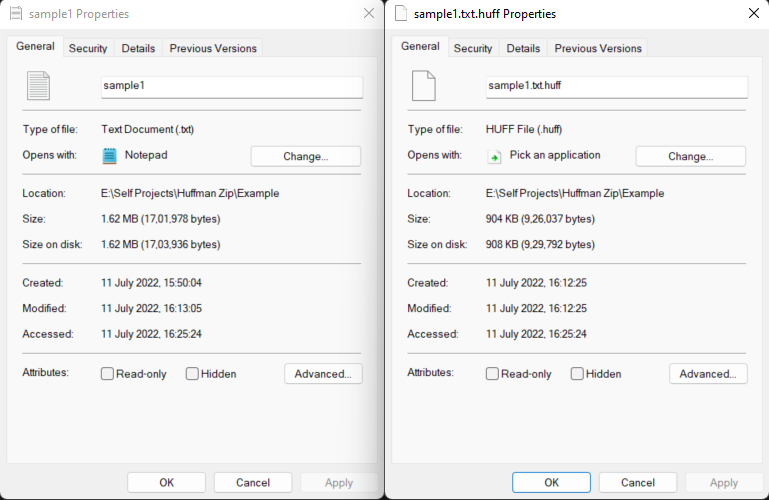
1. Sample1.txt

• Original File size: 17,01,978 bytes
• Compressed File size: 9,26,037 bytes
• Compression Rate: ~45.6%

2. Sample2.txt

• Original File size: 1,26,031 bytes
• Compressed File size: 68,929 bytes
• Compression Rate: ~45.3%

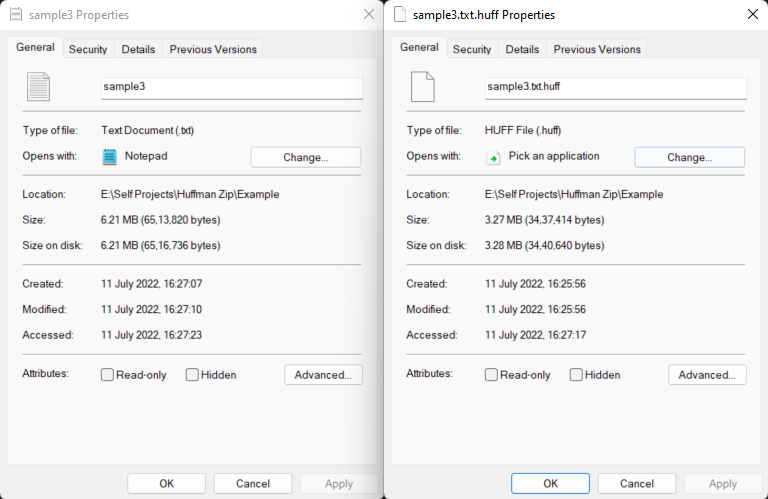
3. Sample3.txt

• Original File size: 65,13,820 bytes
• Compressed File size: 34,37,414 bytes
• Compression Rate: ~47.23%

From this I can conclude the compression rate is around ~46%. Which is not bad!😀

Executing

Well...! for compressed file I have used as '.huff' just short for Huffman, Please do not think this is an unnecessary file😅

Run the batch file:

./Makefile.bat

(or) Execute the command:

gcc -Wall -save-temps "client.c" "encode.c" "decode.c" "huffman.c" -o ""Huffman.exe"

For compressing the file Use -encode as flag For reverting to original file Use -decode as flag

To start executing

./Huffman.exe <flag> <filepath>

Example: For Encoding the sample1.txt file

./Huffman.exe -encode "./Example/sample1.txt"

For decoding the sample1.txt.huff file

./Huffman.exe -decode "./Example/sample1.txt.huff"