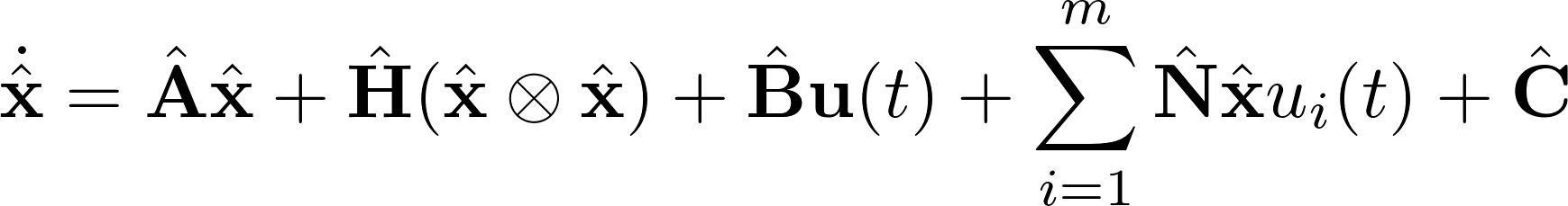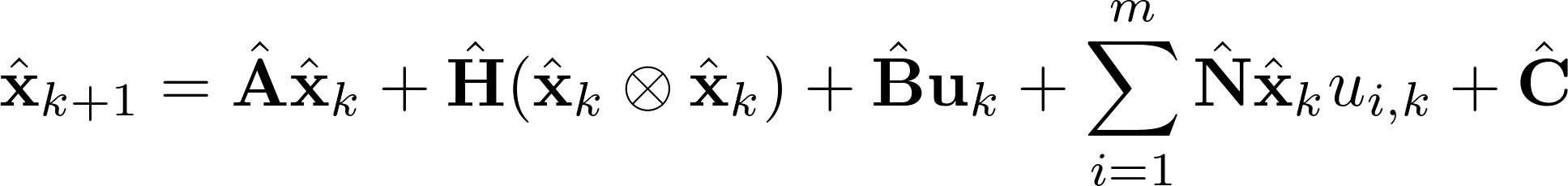Operator Inference

This is a MATLAB implementation of the operator learning approach described in:

1. Peherstorfer, B. and Willcox, K. Data-driven operator inference for non-intrusive projection-based model reduction. Computer Methods in Applied Mechanics and Engineering, 306:196-215, 2016. (Download)

   BibTeX

   @article{Peherstorfer16DataDriven,
   title   = {Data-driven operator inference for nonintrusive projection-based model reduction},
   author  = {Peherstorfer, B. and Willcox, K.},
   journal = {Computer Methods in Applied Mechanics and Engineering},
   volume  = {306},
   pages   = {196-215},
   year    = {2016},
   }

2. Qian, E., Kramer, B., Marques, A., and Willcox, K. Transform & Learn: A data-driven approach to nonlinear model reduction. In the AIAA Aviation 2019 Forum, June 17-21, Dallas, TX. (Download)

   BibTeX

   @inbook{QKMW2019aviation,
   author = {Qian, E. and Kramer, B. and Marques, A. N. and Willcox, K. E.},
   title = {Transform & Learn: A data-driven approach to nonlinear model reduction},
   booktitle = {AIAA Aviation 2019 Forum},
   doi = {10.2514/6.2019-3707},
   URL = {https://arc.aiaa.org/doi/abs/10.2514/6.2019-3707},
   eprint = {https://arc.aiaa.org/doi/pdf/10.2514/6.2019-3707}
   }

3. Qian, E., Kramer, B., Peherstorfer, B., and Willcox, K. Lift & Learn: Physics-informed machine learning for large-scale nonlinear dynamical systems, Physica D: Nonlinear Phenomena, 2020.

   BibTeX

   @article{qian2020lift,
   title={Lift & {L}earn: {P}hysics-informed machine learning for large-scale nonlinear dynamical systems},
   author={Qian, E. and Kramer, B. and Peherstorfer, B. and Willcox, K.},
   journal={Physica D: Nonlinear Phenomena},
   volume={406},
   pages={132401},
   year={2020},
   publisher={Elsevier}
   }

4. Qian, E., Farcas, I.-G., and Willcox, K. Reduced operator inference for nonlinear partial differential equations, in revision, 2021.

Summary

The function inferOperators.m learns a reduced model for the state data X and input data U in the reduced space spanned by the columns of Vr. The data in X are projected onto the space defined by the reduced basis Vr to obtain the reduced state Xhat. Reduced operators are fit to the reduced state data and input data in a least-squares sense.

The learned model in the continuous-time setting can have any of the terms on the right-hand side of the following general model:

In the discrete-time setting the learned model can have any of the terms on the right-hand side of the following general model:

The user specifies whether the model is time-discrete or time-continuous in the argument params.modeltime. The user specifies what types of operators should be fit to the data in the argument params.modelform, which should be a string of characters: L for linear, Q for quadratic, I for input, B for bilinear, and C for constant -- these correspond to the matrices A, H, B, N, and C in the models above, respectively.

For discrete-time models, inferOperators.m assumes that the data in X are an evenly spaced sequence. To handle other types of data the user can provide the optional argument rhs for the least squares solve.

For continuous-time models, inferOperators.m estimates the time derivative dXdt using the timestep params.dt and difference scheme params.ddt_order. See ddt.m for the implemented difference schemes; users may also implement their own. For non-uniform time-spacing, or if exact time derivatives are available, the user can provide the optional argument rhs for the least squares solve. In general, exact time derivative data is ideal and should be used when available.

Examples

The examples folder contains scripts that set-up and run several examples:

• The heat equation example from [1].
• The Burgers' equation from [1].
• The Euler equation example from [3]. This example uses MATLAB's Curve Fitting Toolbox to generate the random initial conditions.
• The heat equation example on a non-uniform grid from [4].

---

This code was developed in MATLAB R2019a and is in a beta state. Please contact Elizabeth Qian (eqian@caltech.edu) with any questions or comments. Boris Kramer also contributed to this code.