Interpolating Neural Networks

This repo contains the source code for observing double descent phenomena with neural networks in empirical asset pricing data.

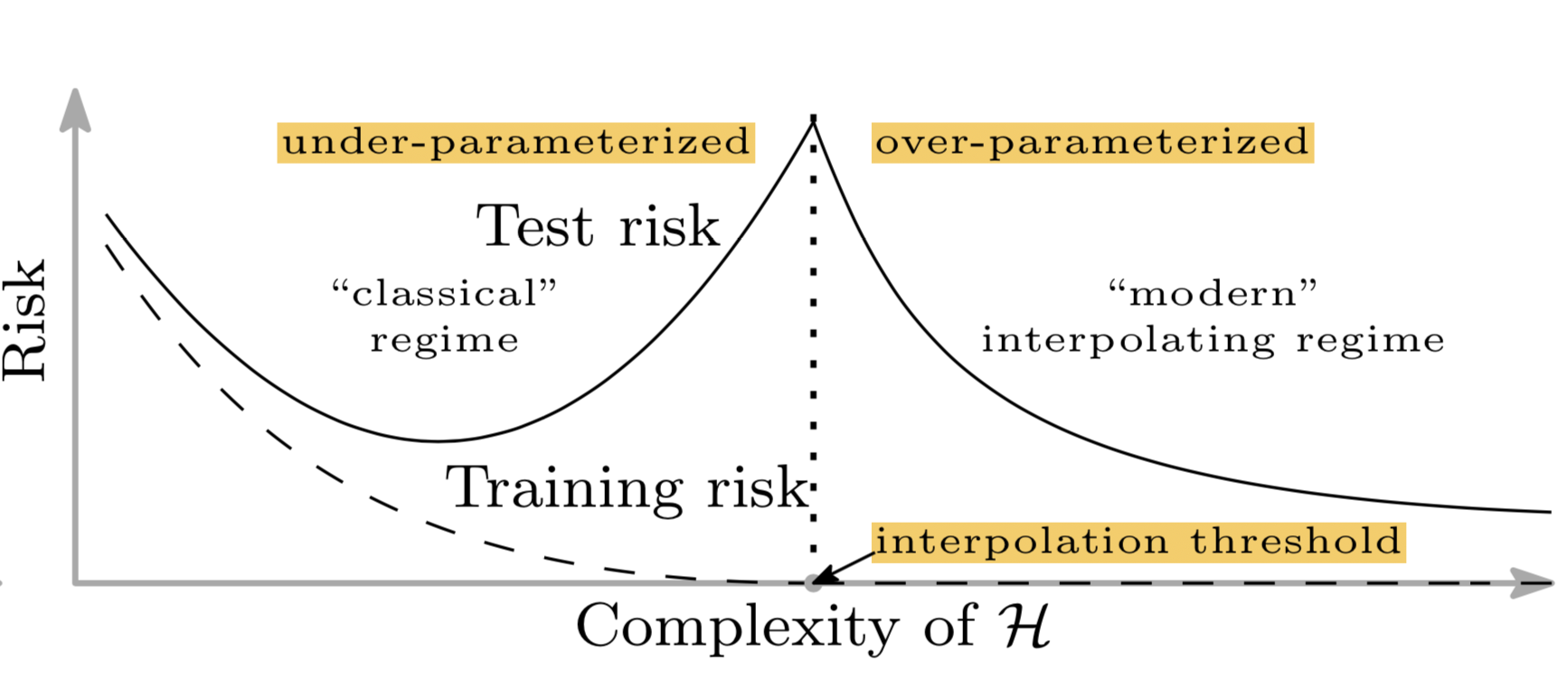Fig. A new double-U-shaped bias-variance risk curve for deep neural networks. (Image source: original paper)

Deep learning models are heavily over-parameterized and can often get to perfect results on training data. In the traditional view, like bias-variance trade-offs, this could be a disaster that nothing may generalize to the unseen test data. However, as is often the case, such “overfitted” (training error = 0) deep learning models still present a decent performance on out-of-sample test data (Refer above figure).

This is likely due to two reasons:

• The number of parameters is not a good measure of inductive bias, defined as the set of assumptions of a learning algorithm used to predict for unknown samples.
• Equipped with a larger model, we might be able to discover larger function classes and further find interpolating functions that have smaller norm and are thus “simpler”.

There are many other explanations of better generalisation such as Smaller Intrinsic Dimension, Heterogeneous Layer Robutness, Lottery Ticket Hypothesis etc. To read more on them in detail, refer Lilian Weng's article.

Usage

In this work, we try to observe double descent phenomena in empirical asset pricing. The observation of double descent is fascinating as financial data are very noisy in comparison to image datasets (good signal to noise ratio).

$ git clone https://github.com/akashsonowal/interpolating-neural-networks/
$ pip install -e .
$ python experiment/run_experiment.py

Notes:

• There are no regularization terms like weight decay, dropout.
• Each network is trained for a long time to achieve zero training risk. The learning rate is adjusted differently for models of different sizes.
• For faster training, GPUs are recommended.

Citation

If you find this method and/or code useful, please consider citing

@misc{interpolatingneuralnetworks,
  author = {Akash Sonowal, Dr. Shankar Prawesh},
  title = {Interpolating Neural Networks in Asset Pricing},
  url = {https://github.com/akashsonowal/interpolating-neural-networks},
  year = {2022},
  note = "Version 0.0.1"
}