Hermite Function Series

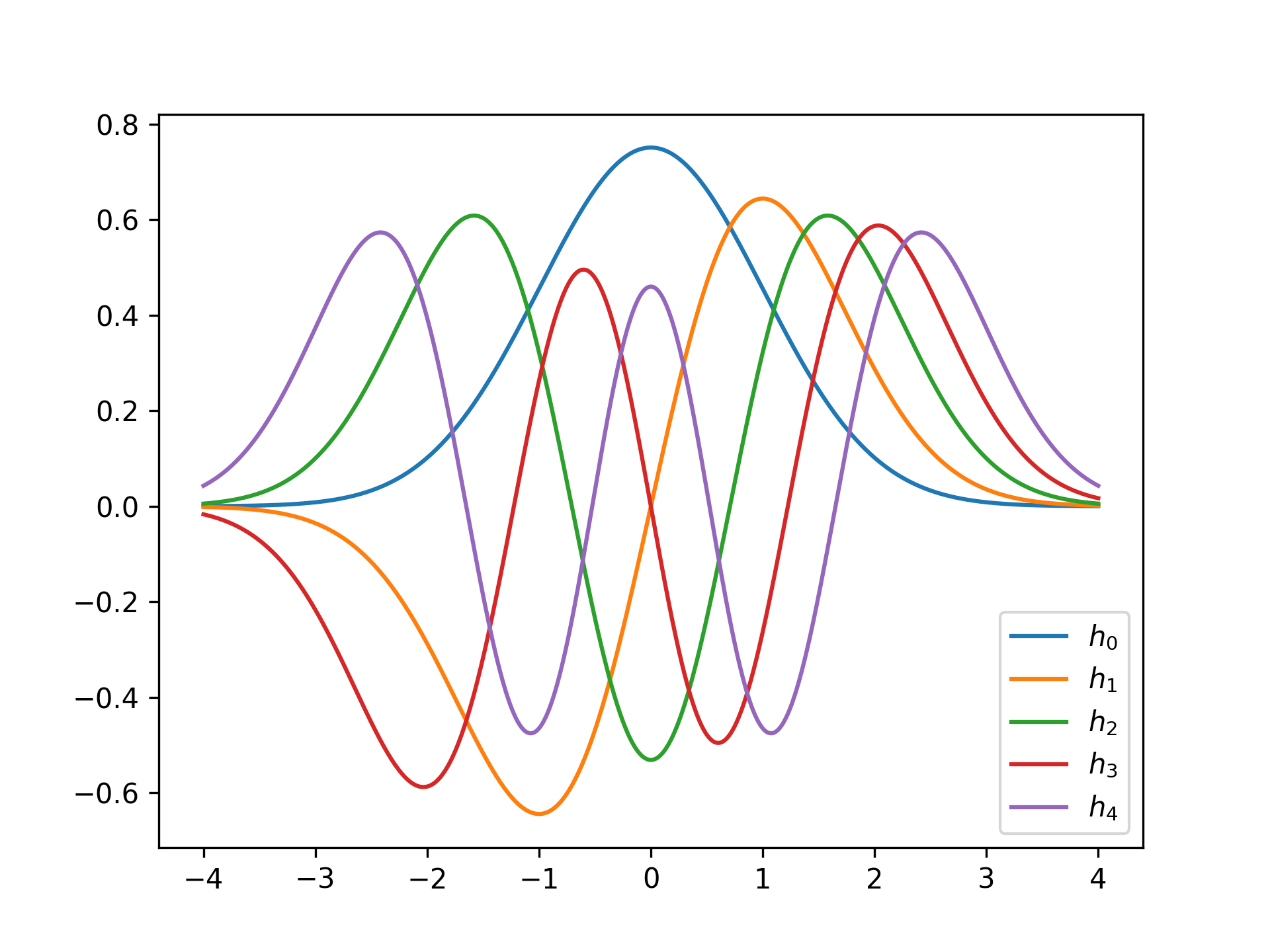
A Hermite function series module.

from hermitefunction import HermiteFunction
import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(-4, +4, 1000)
for n in range(5):
    f = HermiteFunction(n)
    plt.plot(x, f(x), label=f'$h_{n}$')
plt.legend(loc='lower right')
plt.show()

Installation

pip install git+https://github.com/goessl/vector.git
pip install hermite-function

Usage

This package provides a single class, HermiteFunction, to handle Hermite function series.

HermiteFunction extends Vector from the vector module and therefore provides all Hilbert space operations from coefficient access through indexing, over norm calculation to arithmetic.

A series can be initialized in three ways:

• With the constructor HermiteFunction(coef), that takes a non-negative integer to create a pure Hermite function with the given index, or an iterable of coefficients to create a Hermite function series.
• With the random factories HermiteFunction.rand(deg) & HermiteFunction.randn(deg, normed=True) for a random Hermite function series of a given degree.
• By fitting data with HermiteFunction.fit(X, y, deg).

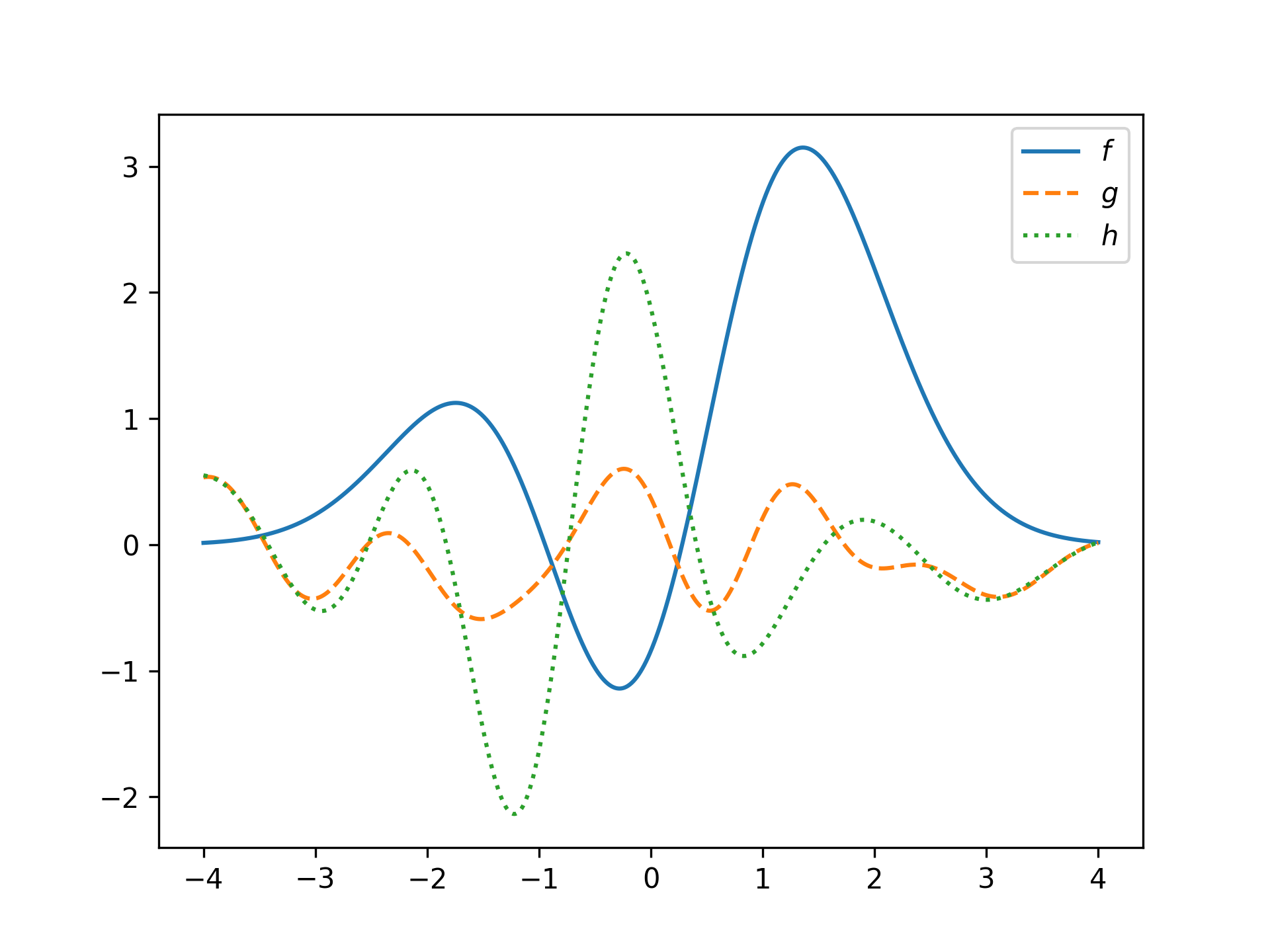
f = HermiteFunction((1, 2, 3))
g = HermiteFunction.randn(15)
h = HermiteFunction.fit(x, g(x), 10)
plt.plot(x, f(x), label='$f$')
plt.plot(x, g(x), '--', label='$g$')
plt.plot(x, h(x), ':', label='$h$')
plt.legend()
plt.show()

Methods for functions:

• evaluation with f(x),
• differentiation to an arbitrary degree f.der(n),
• integration f.antider(),
• Fourier transformation f.fourier() &
• getting the degree of the series f.deg are implemented.

f_p = f.der()
f_pp = f.der(2)
plt.plot(x, f(x), label=rf"$f \ (\deg f={f.deg})$")
plt.plot(x, f_p(x), '--', label=rf"$f' \ (\deg f'={f_p.deg})$")
plt.plot(x, f_pp(x), ':', label=rf"$f'' \ (\deg f''={f_pp.deg})$")
plt.legend()
plt.show()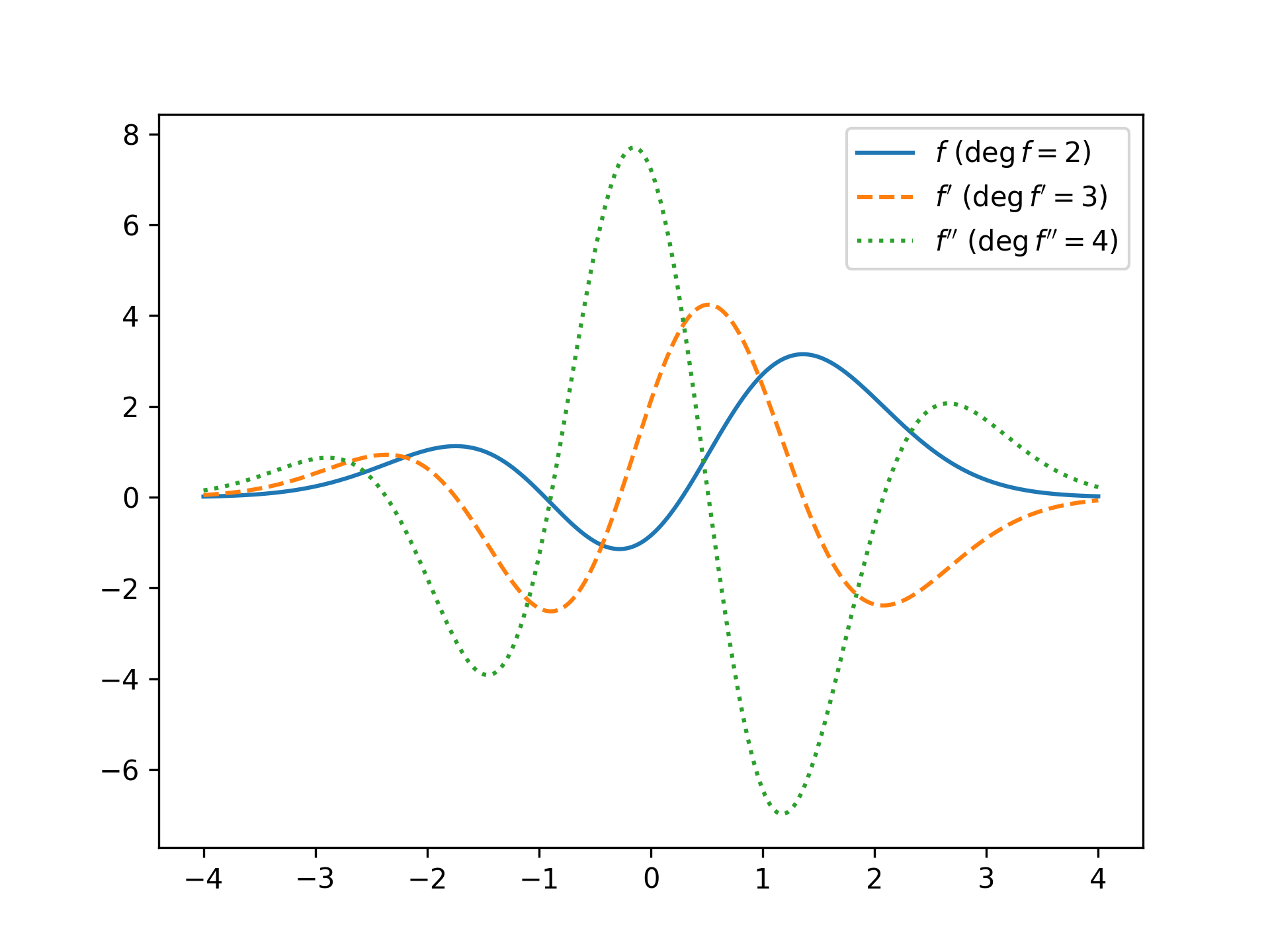

Hilbert space operations inherited from vector

g = HermiteFunction(4)
h = f + g
i = 0.5 * f
plt.plot(x, f(x), label='$f$')
plt.plot(x, g(x), '--', label='$g$')
plt.plot(x, h(x), ':', label='$h$')
plt.plot(x, i(x), '-.', label='$i$')
plt.legend()
plt.show()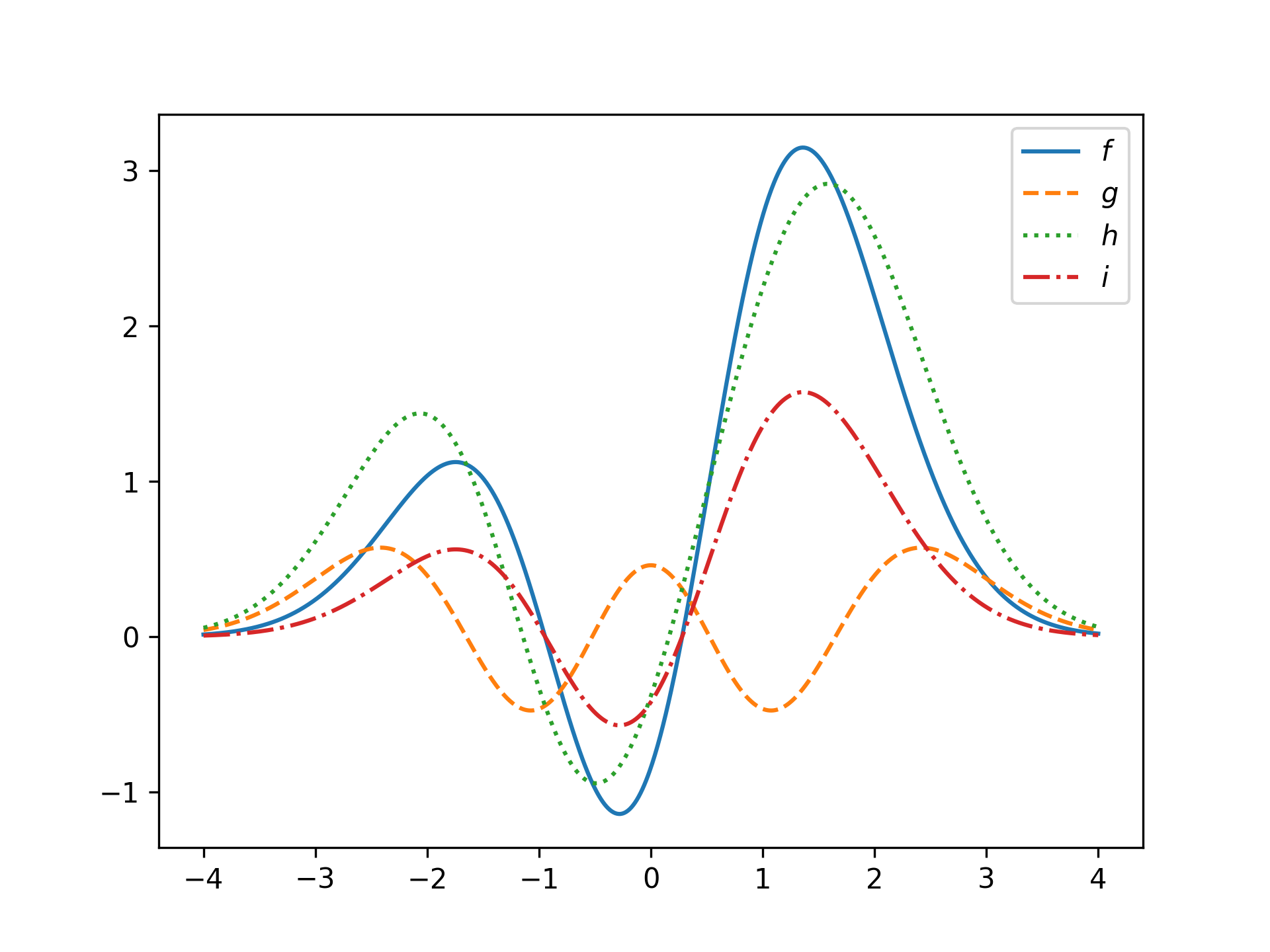

Because this package was intended as a tool to work with quantum mechanical wavefunctions, the expectation value for the kinetic energy is also implemented ($\langle\hat{P}^2\rangle=\frac{1}{2}\int_\mathbb{R}f^*(x)f''(x)dx$, natural units):

f.kin

Proofs

In the following let

$$ f=\sum_{k=0}^\infty f_k h_k, \ g=\sum_{k=0}^\infty g_k h_k. $$

where $h_k$ are the Hermite functions, defined by the Hermite polynomials $H_k$:

$$ h_k(x) = \frac{e^{-\frac{x^2}{2}}}{\sqrt{2^kk!\sqrt{\pi}}} H_k(x) $$

from Wikipedia - Hermite functions.

Differentiation

$$ \begin{aligned} f' &= \sum_k f_k h_k' \\ &\qquad\mid h'_k = \sqrt{\frac{k}{2}}h_{k-1} - \sqrt{\frac{k+1}{2}}h_{k+1} \\ &= \sum_k f_k \left( \sqrt{\frac{k}{2}}h_{k-1} - \sqrt{\frac{k+1}{2}}h_{k+1} \right) \\ &= \sum_{k=0}^\infty f_k\sqrt{\frac{k}{2}} h_{k-1} - \sum_{k=0}^\infty f_k\sqrt{\frac{k+1}{2}} h_{k+1} \\ &\qquad\mid k-1 \to k, \ k+1 \to k \\ &= \sum_{k=-1}^\infty \sqrt{\frac{k+1}{2}}f_{k+1} h_k - \sum_{k=1}^\infty \sqrt{\frac{k}{2}}f_{k-1} h_k \\ &\qquad\mid -0+0 = -\sqrt{\frac{-1+1}{2}}f_{-1+1}h_{-1} + \sqrt{\frac{0}{2}}f_{0-1} h_0 \\ &= \sum_{k=0}^\infty \sqrt{\frac{k+1}{2}}f_{k+1} h_k - \sum_{k=0}^\infty \sqrt{\frac{k}{2}}f_{k-1} h_k \\ &= \sum_k \left( \sqrt{\frac{k+1}{2}}f_{k+1} - \sqrt{\frac{k}{2}}f_{k-1} \right) h_k \end{aligned} $$

With $h'_k=\sqrt{\frac{k}{2}}h_{k+1}-\sqrt{\frac{k+1}{2}}h_{k-1}$ from Wikipedia - Hermite functions.

Integration

With the same relation as above we get

$$ \begin{aligned} h_k' &= \sqrt{\frac{k}{2}}h_{k-1} - \sqrt{\frac{k+1}{2}}h_{k+1} \\ &\qquad\mid +\sqrt{\frac{k+1}{2}}h_{k+1} - h_k' \\ \sqrt{\frac{k+1}{2}}h_{k+1} &= \sqrt{\frac{k}{2}}h_{k-1} - h_k' \\ &\qquad\mid \cdot\sqrt{\frac{2}{k+1}} \\ h_{k+1} &= \sqrt{\frac{k}{k+1}}h_{k-1} - \sqrt{\frac{2}{k+1}}h_k' \\ &\qquad\mid k+1 \to k \\ h_k &= \sqrt{\frac{k-1}{k}}h_{k-2} - \sqrt{\frac{2}{k}}h_{k-1}' \\ &\qquad\mid \int \\ H_k &= \sqrt{\frac{k-1}{k}}H_{k-2} - \sqrt{\frac{2}{k}}h_{k-1} \end{aligned} $$

which can be applied from the highest to the lowest order. For $h_0$ we then get

$$ H_0(x) = \int_{-\infty}^xh_0(x')dx' = \int_{-\infty}^x\frac{e^{-\frac{x'^2}{2}}}{\sqrt[4]{\pi}}dx' = \sqrt{\frac{\sqrt{\pi}}{2}}\text{erf}\left(\frac{x}{\sqrt{2}}\right) \ \left(+\sqrt{\frac{\sqrt{\pi}}{2}}\right) $$

Fourier transformation

Wikipedia - Hermite functions

Kinetic energy

$$ \left\langle\frac{-\hat{P}^2}{2}\right\rangle = -\frac{1}{2}\int_{\mathbb{R}}f^*(x)\frac{d^2}{dx^2}f(x)dx = +\frac{1}{2}\int_{\mathbb{R}}|f'(x)|^2dx = \frac{1}{2}||f'||_{L_{\mathbb{R}}^2}^2 $$

License (MIT)

Copyright (c) 2022 Sebastian Gössl

Permission is hereby granted, free of charge, to any person obtaining a copy of this software and associated documentation files (the "Software"), to deal in the Software without restriction, including without limitation the rights to use, copy, modify, merge, publish, distribute, sublicense, and/or sell copies of the Software, and to permit persons to whom the Software is furnished to do so, subject to the following conditions:

The above copyright notice and this permission notice shall be included in all copies or substantial portions of the Software.

THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE SOFTWARE.