Partitions genome data using the 4-gamete test into a minimal number of blocks which contain no recombinations (=FGT conflicts)
Input is a VCF file, which can represent unphased genotypes, and output is a parsimonious set of breakpoints separating non-overlapping intervals which do not show evidence of recombination, as tested using the four-gamete test.
If you find FGTpartitioner useful for your research, please cite the associated publication:
Chafin, TK. 2020. FGTpartitioner: Parsimonious delimitation of ancestry breakpoints in large genome-wide SNP datasets. Journal of Open Source Software, 5(46), 2030, https://doi.org/10.21105/joss.02030
Of note, there are multiple options for partioning a genome using the four-gamete test. Here are a few, sorry if I left anyone out:
- https://github.com/RILAB/rmin_cut
- https://github.com/YichaoOU/genome_partition
- https://github.com/txje/compatible-intervals
FGTpartitioner is published in the Journal of Open Source Software (see above), and finds the same FGT conflicts as other programs that I have tested. Right now the best solutions for speeding up FGTpartitioner with very large alignments is to use multiprocessing <-t> and to set a maximum physical distance for calculating FGTs <-d>. The justification for the latter is that there exists a certain physical map distance which is almost guaranteed to have spanned multiple recombinations, thus there is no point in continuing to search for FGT conflicts. Ideally you can find some published studies calculating linkage disequilibrium for your species or something similar, and inform this parameter with the larger-end of the expected linkage block size distribution.
Requires Python 3 and the following modules:
- pyVCF
- pySAM
- intervaltree
- Cython > 0.27
- pathos
- tabix
You will additionally need tabix installed to block-compress and index your VCF file (which enables me to parse it more quickly).
The easiest way to install all of the dependencies is through conda:
conda install -c conda-forge -c bioconda pyvcf intervaltree cython pathos pysam tabix
If you don't have conda installed, go here and choose the correct Python3 installer for your system.
To prep FGTpartioner for running, you will first need to pre-compile the cythonized portions of the code:
python setup.py build_ext --inplace
After that, FGTpartitioner is ready to run. You can view the help menu by typing:
./FGTpartitioner.py -h
Note that this assumes your python installation is in /usr/bin/env. If for example you are using a local anaconda python installation, you can provide a path to the python interpreter:
~/anaconda/bin/python3 FGTpartitioner.py -h
Or, if your local python is in your $PATH:
python3 FGTpartitioner.py -h
The input file (provided via -v) is a standard VCF file, including contig lengths in the ##contig headers. You can find an example of a VCF file in the examples/ directory. In short, a minimally conforming VCF should have the following structure:
##fileformat=VCFv4.2
##contig=<ID=chr1.scaffold1,length=10000>
##FORMAT=<ID=GT,Number=1,Type=Integer,Description="Genotype">
##FORMAT=<ID=GP,Number=G,Type=Float,Description="Genotype Probabilities">
##FORMAT=<ID=PL,Number=G,Type=Float,Description="Phred-scaled Genotype Likelihoods">
#CHROM POS ID REF ALT QUAL FILTER INFO FORMAT SAMP001 SAMP002 SAMP003 SAMP004
chr1.scaffold1 100 rs11449 G A . PASS . GT 0/0 0/0 1/1 1/1
chr1.scaffold1 200 rs11449 T A . PASS . GT 0/0 1/1 0/0 1/1
chr1.scaffold1 300 rs84825 A T . PASS . GT 0/0 1/1 1/1 1/1
chr1.scaffold1 400 rs84825 A G . PASS . GT 1/1
...
...
...
You will also need to block-compress and index your VCF file to speed up parsing:
#Run bgzip (NOT gzip) to compress your joint VCF file
bgzip file.vcf
#tabix to index it
tabix -h -f -p vcf file.vcf.gz
The result will be a binary compressed-VCF ".vcf.gz" file, and a ".vcf.gz.tbi" index file. The ".vcf.gz" will be the input provided to FGTpartitioner using the -v flag, and the '.vcf.gz.tbi" file should be in the same directory, and with the same prefix.
You can view all of the possible options by calling the help menu in the command-line interface:
tyler:FGTpartitioner $ ./FGTpartitioner.py -h
Must provide VCF file <-v,--vcf>
FGTpartitioner.py
Contact:Tyler K. Chafin, tylerkchafin@gmail.com
Usage: FGTpartitioner.py -v <input.vcf> -r <1|2|3> [-c chr1]
Description: Computes parsimonious breakpoints to partition chromosomes into recombination-free blocks
Arguments:
-v : VCF file for parsing
-r : Strategy to treat heterozygotes. Options:
1: Randomly haploidize heterozygous sites
2: Fail FGT if heterozygote might be incompatible
3: Pass FGT if heterozygote might be compatible
-c : Chromosome or contig in VCF to partition
-o : Output file name [default: regions.out]
-t : Number of threads for parallel execution
-m : Minimum number of individuals genotyped to keep variant [default=2]
-a : Maximum number of alleles allowed per locus [default=2]
-h : Displays help menu
One important option which you will need to consider is <-r>, which determines how FGTpartitioner behaves when it encounters heteroozygotes. The four-gamete test has several assumptions, the most important being: 1) That you have sampled haploid chromosomes; and 2) an infinite-sites mutation model (e.g. all mutations occur at a new site- no back mutation, or multiple mutations per site). You can find more details below in the "Four-Gamete Test" section.
In order to meet assumption #1, we need to manipulate our unphased genotype data. FGTpartioner allows 3 ways in which this can be accomplished (passed as an integer option to the -r flag): 1) <-r 1> Randomly choose one allele and treat the sample as homozygous for that allele, at that position; 2) <-r 2> Ask if either allele causes a failure of the four-gamete test, and treat the comparison as failed if so (e.g. a pessimistic/safe approach); or 3) <-r 3> ask if either allele could possibly be consistent with the four-gametes assumption, and pass the comparison if so (e.g. an optimistic approach). This pessimistic/optimistic approach was inspired by Wang et al (2010)
Some test data for verifying the function of FGTpartitioner are presented in the examples/ directory.
To run a simple test case, you can use the included examples/example_1.vcf file. You could generate the required block-compressed VCF and index files like so (although these are already provided for you: examples/example_1.vcf.gz and examples/example_1.vcf.gz.tbi):
cd examples
bgzip example_1.vcf
tabix -h -f -p vcf example_1.vcf.gz
cd -
To run a simple case, with all sites passing if any possible heterozygote resolution works (see below in documentation):
python FGTpartitioner.py -v examples/example_1.vcf.gz -r 3 -o out.txt
The screen output of FGTpartitioner would look like so:
Opening VCF file: examples/example_1.vcf.gz
Reading all chromosomes from VCF...
Diploid resolution strategy: Optimistic (change with -r)
Number of process threads: 1 (change with -t)
Minimum genotyped individuals to consider locus: 2 (change w/ -m)
Starting FGT sweeps.....
Performing FGT check on: chr1.scaffold1
Chromosome chr1.scaffold1 skipped 1 sites for too much missing data.
Chromosome chr1.scaffold1 skipped 1 sites for too many alleles.
Chromosome chr1.scaffold1 found 10 passing variants.
Seeking intervals across chr1.scaffold1 using 1 threads.
Found 4 intervals.
Resolving FGT incompatibilities...
Found 3 most parsimonious breakpoints.
Writing regions to file (format: chromosome:start-end)
Note that these are 1-based indexing (VCF is 0-based)
Done
Before starting work, this reports the diploid resolution strategy (here "Optimistic" for <-r 3>), the number of process threads, and the number of individuals required to consider a SNP, as well as the correct flags required to modify those values. Next, FGTpartitioner reports the number of sites skipped (if any), as well as the number of intervals found, and number of parsimonious breakpoints required to resolve all intervals.
This would produce the following "out.txt", formatted as chromosome:start-end, with 1-based indexing (note that FGTpartitioner will remind you of this format in the terminal output):
$cat out.txt
chr1.scaffold1:1-150
chr1.scaffold1:151-300
chr1.scaffold1:301-10001
To run with 4 threads (-t), a minimum of 4 genotyped samples per site (-m), and a maximum considered distance of 200 bases (-d):
python FGTpartitioner.py -v examples/example_1.vcf.gz -r 3 -o out.txt -t 4 -m 3 -d 200
This produces the following output:
Opening VCF file: examples/example_1.vcf.gz
Reading all chromosomes from VCF...
Diploid resolution strategy: Optimistic (change with -r)
Number of process threads: 4 (change with -t)
Minimum genotyped individuals to consider locus: 3 (change w/ -m)
Starting FGT sweeps.....
Performing FGT check on: chr1.scaffold1
Chromosome chr1.scaffold1 skipped 2 sites for too much missing data.
Chromosome chr1.scaffold1 skipped 1 sites for too many alleles.
Chromosome chr1.scaffold1 found 9 passing variants.
Seeking intervals across chr1.scaffold1 using 4 threads.
Merging results from child processes...
Found 3 intervals.
Resolving FGT incompatibilities...
Found 3 most parsimonious breakpoints.
Writing regions to file (format: chromosome:start-end)
Note that these are 1-based indexing (VCF is 0-based)
Done
Note that the number of passed sited decreased (9 from 10), reflecting the more stringent gentotype filter (-m 4), as did the number of intervals which were found. The resulting out.txt recovered the same intervals in this case:
$cat out.txt
chr1.scaffold1:1-150
chr1.scaffold1:151-300
chr1.scaffold1:301-10001
If you do not get these exact same outputs, something may not be working. Feel free to post an issue here on github, or email me at tkchafin(@)uark.edu for help. Please include your exact commands and outputs, including any error messages you receive.
The output of FGTpartitioner is a list of regions in GATK format (chromosome:start-end), in a 1-based indexing scheme:
CM000001.3:1-218120
CM000001.3:218121-218432
CM000001.3:218433-221068
CM000001.3:221069-224784
CM000001.3:224785-228655
...
...
...
You can then use these to subset your VCF using your choice of tool. I usually use vcftools and bcftools for manipulating VCF files.
If you want to ultimately parse multiple sequence alignments from your VCF file and the FGTpartitioner outputs, I would recommend my tool vcf2msa.py.
To get an average region size, you can use the following bash command:
less regions.out | sed "s/.*://g" | awk 'BEGIN{FS="-"}{print $2-$1}' |awk 'BEGIN{sum=0; count=0; sumsq=0}{count+=1; sum +=$1; sumsq+=$1*$1}END{print(sum/count); print sqrt(sumsq/count - (sum/count)**2)}'
The general principle of the four-gamete test (FGT) is this: If we've sampled two positions (SNPs) along a chromosome, assuming that multiple mutations at a site never occur (= 'infinite sites' assumption), the ONLY way that we could possibly sample haploid chromosomes exhibiting all combinations of alleles at those two positions is if recombination had occured.
For example, if we sampled two SNPs on a chromosome, one at position 1028 which is either an A or a T, and another at position 4589 which is either a G or a C:
| Position | Allele1 | Allele2 |
|---|---|---|
| 1028 | A | T |
| 4589 | G | C |
It should be impossible to observe all possible combinations of A/T and G/C (i.e. A at position 1 and G at position 2, A as position 1 and C at position 2, and so on...) without one of two things occuring: 1) There have been multiple convergent substitutions at a site (see: homoplasy); or 2) A crossover event has occured, allowing chromosomes to exchange alleles. Since the FGT assumes that #1 never occurs (the infinite sites assumption), then we must conclude that #2 has occured.
Conducting the test is simple. If we sample at least 4 haploid chromosomes, we shouldn't see all four possible combinations of alleles. For example, the following sampled chromosomes do NOT violate the four-gamete test:
| Sample | 1028 Allele | 4589 Allele |
|---|---|---|
| 1 | A | C |
| 2 | A | C |
| 3 | A | C |
| 4 | T | G |
Here, only 2 combinations are seen here. One haplotype, found in samples 1-3, has ----A--------C----, while the other haplotype (sample 4) has ----T--------G----. However, if we sampled the following chromosomes:
| Sample | 1028 Allele | 4589 Allele |
|---|---|---|
| 1 | A | G |
| 2 | A | C |
| 3 | T | C |
| 4 | T | G |
We see that all possible combinations were sampled:
----A--------C----
----A--------G----
----T--------C----
and
----T--------G----
This is only possible (again, given an assumption that multiple substitutions per site never occurs), if at some point there had been a crossover event duyring meiosis allowing recombination between these two sites:
----A--------C---- --> ----A---\/----C---- --> ----A--------G----
----T--------G---- --> ----T---/\----G---- --> ----T--------C----
Meaning, in this sample of 4 chromosomes, all possible gametes resulting from this recombination event are seen. Understanding this should demonstrate the difficulty of applying the four-gamete test to an unphased diploid sample: What do we do with heterozygotes?
If we sample the following unphased genotype: ----A/T--------C/G---- (where A/T and C/G represent heterozygous genotypes).
How do we know the haplotypes of the two individual chromosomes? The short answer is, given this data alone, that we can't. That is why I give 3 options in FGTpartitioner:
-r 1 This option randomly resolves heterozygotes, yielding one of the following as a pseudo-haplotype for this sample:
----A--------C----
----A--------G----
----T--------C----
----T--------G----
-r 2 This option considers all possible pseudo-haplotypes for this sample, and fails the FGT if any of these would violate the FGT.
-r 3 This option considers all possible pseudo-haplotypes for the sample, and optimistically assumes that if any of them could be consistent with the FGT, that recombination did not occur.
While not ideal, in the absence of phasing information (as is often the case when dealing with non-model data) we don't have many options.
The basic idea is that we perform a minimal number of pairwise comparisons between SNPs so as to characterize any possible recombination events which might have occured, and then place a minimal number of breakpoints along the chromosome to yield a parimonious set of blocks which do not contain variants violating the FGT.
That is to say that, none of these blocks appear to contain recombination events according to a relatively low-power test (the FGT). I also use a 'greedy' approach in that I retain all variant information. As a result, these blocks likely do contain recombinations, but the FGT lacks the power to identify it.
When identifying FGT violations, I place these as intervals in an interval tree data structure, which is an efficient way of storing and parsing this sort of data. For each SNP-pair which violate the FGT, I also assign a layer (k) representing the number of SNPs (since these are the only informative columns in the alignment) which are subsumed by the interval. For example, if the A/C and A/T SNPs in the following violated the FGT, the interval length (k), or the number of SNPs spanned, would be 5.
_________________________________________________
--------A/T----------T/C----T/C----G/A---C/T------------A/C--------T/G--
With increasing distance between SNPs, the higher probability that multiple recombination events have occured. For this reason, if multiple "conflict intervals" overlap, I place a higher weight on the interval with the minimum-k:
_________________________________________________
_______
--------A/T----------T/C----T/C----G/A---C/T------------A/C--------T/G--
In this example, two conflicts were found: one of k=1 and another of k=5. To "solve" this interval tree (i.e. place the smallest number of breakpoints so as to eliminate all FGT conflicts), I solve from min(k) to max(k). Here, FGTpartitioner would find the following solution:
__________________|_______________________________
____|___
--------A/T----------T/C--|--T/C----G/A---C/T------------A/C--------T/G--
Where "|" represents the breakpoint. The algorithm first considers the k=1 interval, and places a breakpoint in the center between the flanking SNPs. This breakpoint also resolves the k=5 interval, thus solving the alignment to create two blocks (one breakpoint), which is the most parsimonious solution. In reality, we do not know where the breakpoint actually occured: it could be anywhere within the k=1 interval. My solution was to evenly divide these monomorphic nucleotides between the two breakpoints. This might not be your desired behavior... But fortunately this would be very easy to change in the code- have at it.
In reality, FGTpartitioner actually considers every possible breakpoint (centerpoint between SNPs, or "nodes"), so as to maximally resolve intervals. For example, with the following case:
_______________________________________________________
_________________________________________
____________________
--------A/T----------T/C--(1)--T/C--(2)--G/A---C/T------------A/C--------T/G--
The algorithm would look at centerpoint #1, count the number of intervals which would be resolved (=2), and then do the same for centerpoint #2 (=3). In this case, the most parsimonious solution is to place a single breakpoint at candidate #2.
Because of this strategy, you might have noticed that it would be a waste of time to consider any pairwise comparisons after identifying a conflict, because those intervals would always be of larger k (and thus never considered, since we solve from min(k) to max(k)). So, I don't actually consider all possible comparisons, but instead consider sequentially more distance SNPs until I find a conflict- which will be guaranteed to be the minimal-k conflict for the focal SNP. Starting from the first SNP, I would make passes until discovering a conflict:
Pass #1 ==============>
Pass #2 =====================>
Pass #3 ============================>
...
...
--------A/T----------T/C----T/C----G/A---C/T------------A/C--------T/G--
The same procedure is then performed for each SNP:
Pass #1 =======>
Pass #2 ==============>
Pass #3 ====================>
...
...
--------A/T----------T/C----T/C----G/A---C/T------------A/C--------T/G--
There are probably better ways to do it, but this accomplishes my goal so ¯_(ツ)_/¯
To efficiently process very large alignments, FGTpartitioner is best used on an HPC system.
For example, with a very large full-chromosome alignment for a mammalian dataset, comprising >2,000,000 variants, FGTpartitioner peaked at about 18GB memory usage.
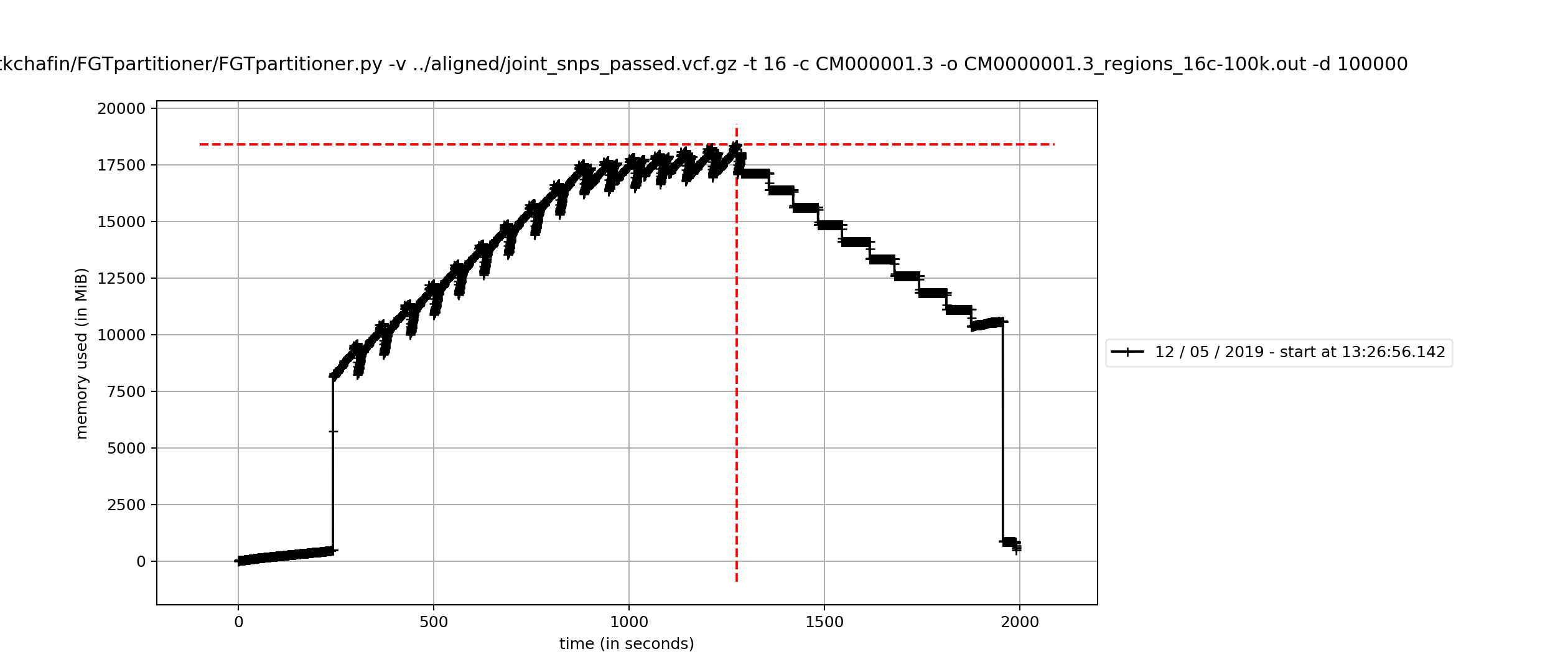Note that this will be effected by the number of cores, with less cores requiring less memory.
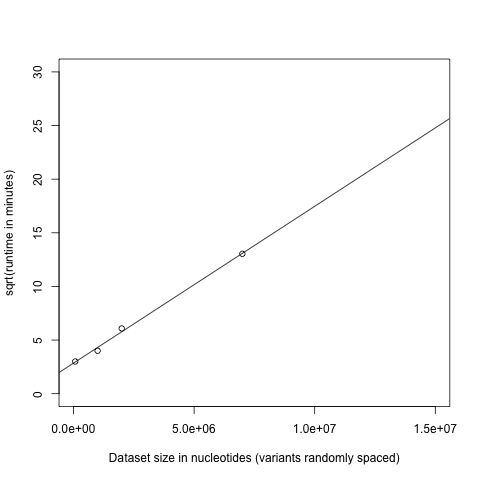
Predicting the runtimes for FGTpartitioner is difficult, as it will depend on both the number of variants, and the number of them showing FGT conflicts (which increases the time for finding the most parsimonious breakpoints).
Runtimes in general will scale n^2 with dataset size:
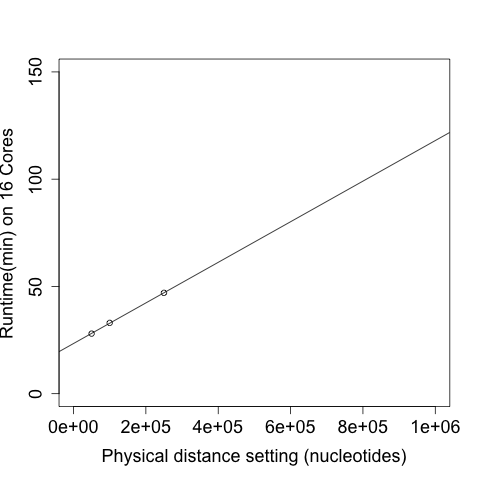
This can be helped by using the <-d> makimum allowable distance, which produced a linear speed-up:
Note that these were calculated on a fairly large alignment of ~2 million variants. See above for how dataset size will effect runtimes.
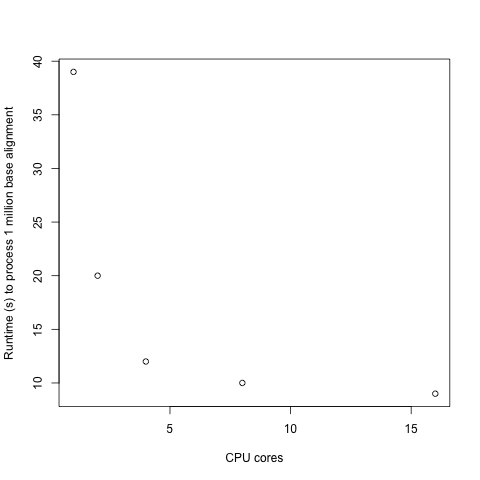
FGTpartitioner shows diminishing returns with added processors, with adding a second core generally halving the runtime, while adding a 16th core does very little:
As such, if you have limited cores available but very large amount of sequence to process, a better investment of your available cores would be to use a modest amount (2-4) per chromosome (selected using -c), and to run individual chromosomes in separate FGTpartitioner runs.
One way you could do this would be with the excellent GNU Parallel tool:
parallel `python3 FGTpartitioner.py -i input.vcf.gz -t 2 -c {} -o {}_regions.out' ::: {chr1 chr2 chr3 chr4}
The above would dedicate 2 cores each to 4 separate FGDpartitioner runs (one for each of 4 chromosomes). You can read more on the use of GNU Parallel here
Performance benchmarking was conducted for FGTpartitioner and similar methods using publicly available data from the NCBI SRA. I ran tests using a 4-taxon alignment of Canis lupus chromosome 1 (~120 Mb), generated from raw reads (C. lupus: SRR7107787; C. rufus: SRR7107783; C. latrans: SRR1518489; Vulpes vulpes: SRR5328101-115). Reads were first aligned with bowtie2 (Langmead & Salzberg, 2012) and subsequently genotyped using the HaplotypeCaller and best practices from GATK (McKenna et al., 2010). Tests were all conducted within a 64-bit Linux environment, on machines equipped with dual 8-core Intel Xeon E5-4627 3.30GHz processors and 265GB RAM.
Memory usage for processing a full alignment with FGTpartitioner on 16 cores peaked at 18GB (with less memory required when using fewer cores). Total runtime scales linearly with the maximum allowable physical distance between SNPs to check for four-gamete conditions, with <-d 250000> taking ~50 minutes and <-d 100000> taking 36 minutes to process an alignment comprising >2 million variants. Increasing number of cored offer diminishing returns, with 1, 2, 4, 8, and 16 cores taking 39, 20, 12 , 10, and 9 minutes, respectively (to process a 1 million base subset of the 4-taxon chromosome 1 alignment). Runtimes also scale linearly with dataset size (in total variants). Haplotype resolution strategy (random, pessimistic, or optimistic) was not found to impact runtimes.
For comparison, I attempted to delimit recombinatorial genes using an alternate method based on the four-gamete test, RminCutter.pl (https://github.com/RILAB/rmin_cut). Because RminCutter does not handle diploid data, I created pseudohaplotypes by randomly resolving heterozygous sites (pseudoHaploidize.py; https://github.com/tkchafin/scripts). I also ran the MDL approach (Ané, 2011), which uses a parsimony criterion to assign breakpoints separating phylogenetically homogenous loci, while penalizing for the number of breakpoints. Neither MDL nor RminCutter could complete an analysis on the full chromosome 1 dataset in a reasonable time span (capped at 10 days), so I first divided the alignment into blocks of ten-thousand parsimony-informative sites each (as these determine runtime, not total length). This produced 21 sub-alignments. MDL took 24 hours across 48 cores to complete a single 5 Mb segment, thus was not further explored. RminCutter.pl took an average of 22 hours per segment (single-threaded). Of note, RminCutter and FGTpartitioner yielded identical results when using comparable settings restricted to a pseudo-haploid dataset. FGTpartitioner thus offers an efficient and methodologically simple solution for ancestry delimitation in non-model diploid organisms with large genomes.
- Ané, C. (2011). Detecting phylogenetic breakpoints and discordance from genome-wide alignments for species tree reconstruction. Genome Biology and Evolution, 3(1), 246–258. doi:10.1093/gbe/evr013
- Langmead, B., & Salzberg, S. L. (2012). Fast gapped-read alignment with Bowtie 2. Nature Methods. doi:10.1038/nmeth.1923 McKenna, A., Hanna, M., Banks, E., Sivachenko, A., Cibulskis, K., Kernytsky, A., … DePristo, M. A. (2010). The Genome Analysis Toolkit: a MapReduce framework for analyzing next-generation DNA sequencing data. Genome Research. doi:10.1101/gr.107524.110
Copyright © 2019 Tyler K. Chafin tylerkchafin@gmail.com
This program is free software: you can redistribute it and/or modify it under the terms of the GNU General Public License as published by the Free Software Foundation, either version 3 of the License, or (at your option) any later version.
This program is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details.
You should have received a copy of the GNU General Public License along with this program. If not, see https://www.gnu.org/licenses/.