This is a simple NN project written in Octave consist of only one hidden layer(simplest version of Neural-Network). It is for educational purposes in order for the public to understand the math structure behind neural networks. It is a university course project in Machine_Learning so it is developed without a NN-library or a toolkit.
I prefer Octave instead of Matlab due to it is part of Gnu/fsf project and stable for your machine
Open a terminal and type :
sudo add-apt-repository ppa:octave/stable
sudo apt-get update
sudo apt-get install octave
The NN detects handwritten numbers that are included in mnist_data.
The main script is the 'demo_mnistLogreg.m' file which loads the data from the mnist_all.mat, splits them into training_set and test_set, normalizes the pixels to take values in [0,1] , and uses the other main functions such as costgrad_softmax, ml_softmax , etc.
The main purpose is to detect the handwritten numbers and this will be done with multiple logistic regressions which will classify the data we have. The idea is to take a large number of handwritten digits, known as training examples, and then develop a system which can learn from those training examples. In other words, the neural network uses the examples to automatically infer rules for recognizing handwritten digits.
The data we have looks like... :
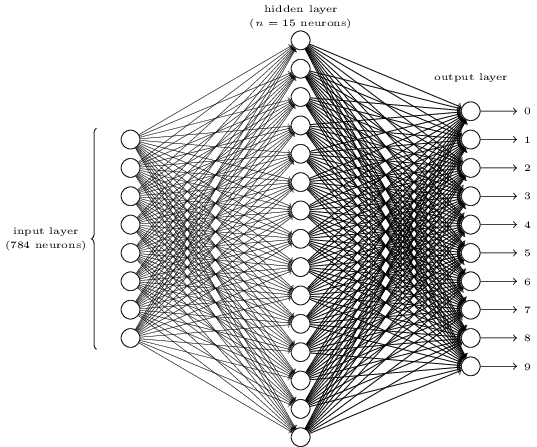
To recognize individual digits we will use a three-layer neural network. The first layer is the input layer, the second is the hidden layer and the third is the output layer.
-
The input layer of the network contains neurons that are encoding the values of the input pixels. As discussed in the next section, our training data for the network will consist of many 2828 by 2828 pixel images of scanned handwritten digits, and so the input layer contains 784=28×28neurons.
-
The second layer of the network is the hidden layer. We denote that the number of neurons in this hidden layer equals n , and we will experiment with different values for n.
-
The output layer of the network contains 10 neurons. If the first neuron triggers, for example, has an output ≈1, then that will indicate that the network thinks the digit is a 0. If the second neuron triggers then that will indicate that the network thinks the digit is a 1. And so on. A little more specifically, we numerate the output neurons from 0 to 9, and then figure out which neuron has the highest activation value. If that neuron is, let's say, neuron number 6, then our network will guess that the input digit was a 5. And so on for the other output neurons.
This is an image of NN structure :
the hidden units in this image are 15 but the default number of hidden units in the project is n = 250
The results of the tests-combinations with different numbers of hidden_units , number of iterations and λ(lambda) :